A surprising explanation for generalization in neural networks
Recent research is increasingly investigating how neural networks, being as hyper-parametrized as they are, generalize. That is, according to traditional statistics, the more parameters, the more the model overfits. This notion is directly contradicted by a fundamental axiom of deep learning:
Increased parametrization improves generalization.
Although it may not be explicitly stated anywhere, it’s the intuition behind why researchers continue to push models larger to make them more powerful.
There have been many efforts to explain exactly why this is so. Most are quite interesting; the recently proposed Lottery Ticket Hypothesis states that neural networks are just giant lotteries finding the best subnetwork, and another paper suggests through theoretical proof that such phenomenon is built into the nature of deep learning.
Perhaps one of the most intriguing, though, is one proposing that deeper neural networks lead to simpler embeddings. Alternatively, this is known as the “simplicity bias” — neural network parameters have a bias towards simpler mappings.
Minyoung Huh et al proposed in a recent paper, “The Low-Rank Simplicity Bias in Deep Networks”, that depth increases the proportion of simpler solutions in the parameter space. This makes neural networks more likely — by chance — to find simple solutions rather than complex ones.
On terminology: the authors measure the “simplicity” of a matrix based on its rank — roughly speaking, a measurement of how linearly independent parts of the matrix are on other parts. A higher rank can be considered more complex since its parts are highly independent and thus contain more “independent information”. On the other hand, a lower rank can be considered simpler.
Huh et al begin by analyzing the rank of linear networks — that is, networks without any nonlinearities, like activation functions.
The authors trained several linear networks of different depths on the MNIST dataset. For each network, they randomly drew 128 neural network weights and the associated kernel, plotting their ranks. As the depth increases, the rank of the network’s parameters decreases.
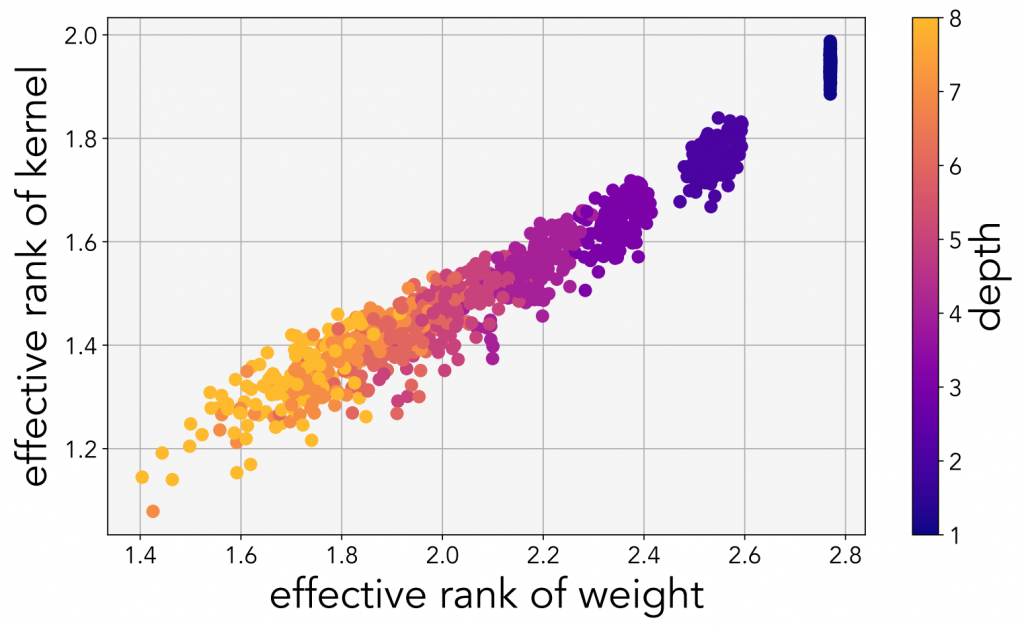
This can be derived from the fact that the rank of the product of two matrices can only decrease or remain the same from the ranks of each of its constituents. If we get a little bit more abstract, we can think of this intuitively as: each matrix contains its own independent information, but when they are combined, the information of one matrix can only get muddled and entangled with the information in another matrix.
rank(AB) ≤ min (rank(A), rank(B))
What is more interesting, though, is that the same applies to nonlinear networks. When nonlinear activation functions like tanh or ReLU are applied, the pattern is repeated: higher depth, lower rank.
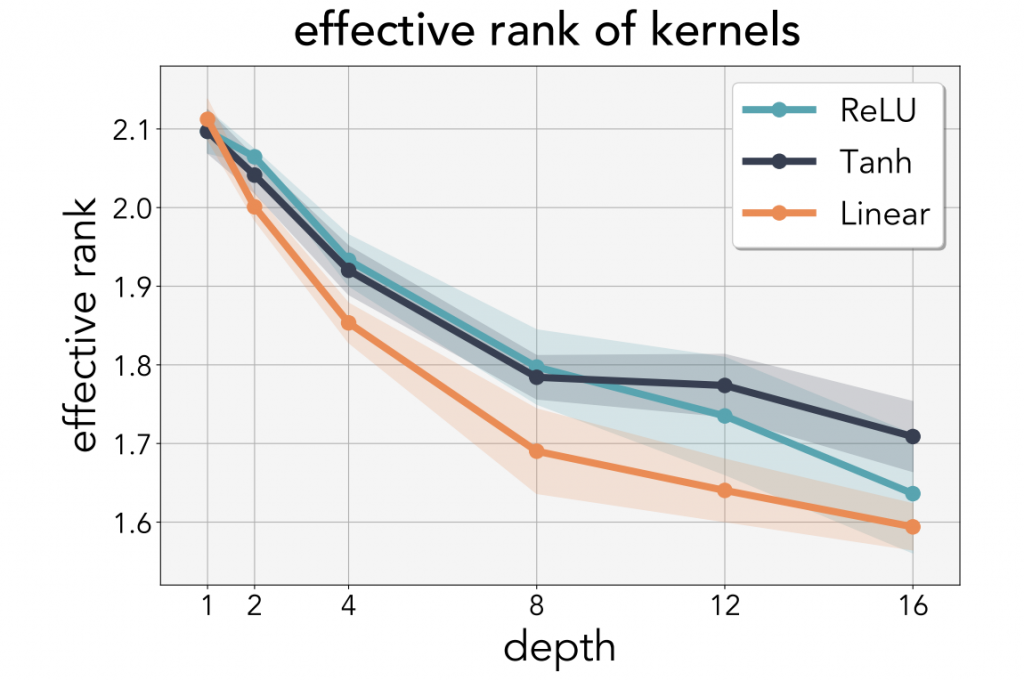
The authors also performed hierarchical cluster kernels for different depths of the network for the two nonlinearities (ReLU and tanh). As the depth increases, the presence of block structures shows decreasing rank. The “independent information” each kernel carries decreases with depth.
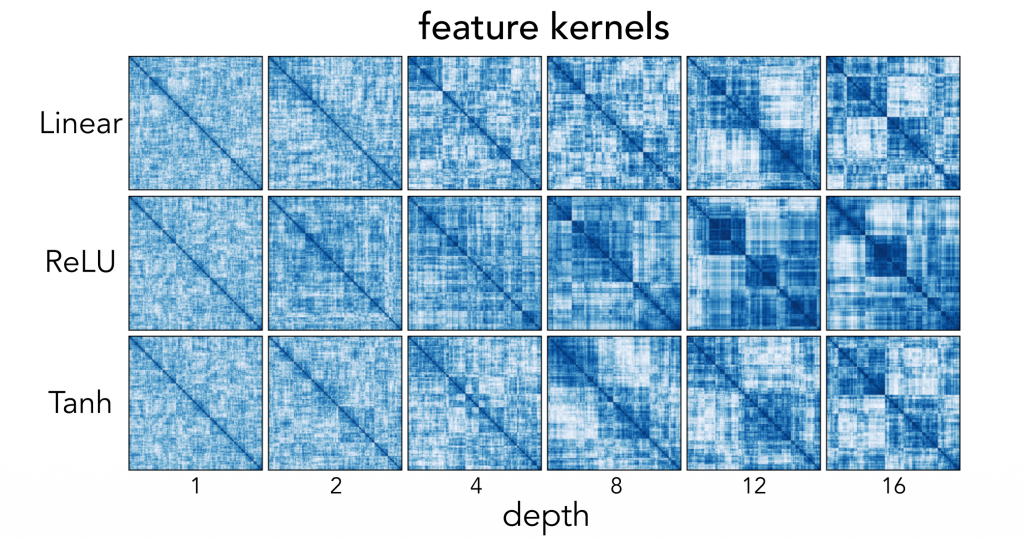
Hence, although it may seem odd, over-parametrizing a network acts as implicit regularization. This is especially true with linearities; thus, a model’s generalization can be improved by increasing linearities.
In fact, the authors find that on both the CIFAR-10 and CIFAR-100 datasets, linearly expanding the network increases accuracy by 2.2% and 6.5% from a baseline simple CNN. On ImageNet, linear over-parametrization of AlexNet increases accuracy by 1.8%; ResNet10 accuracy increases by 0.9%, and ResNet18 accuracy increases by 0.4%.
This linear over-parametrization — which is not adding any serious learning capacity to the network, only more linear transformations — performs even better than explicit regularizers, like penalties. Moreover, this implicit regularization does not change the objective being minimized.
Perhaps what is most satisfying about this contribution is that it is in agreement with Occam’s razor — a statement many papers have questioned or outright refuted as being relevant to deep learning.
The simplest solution is usually the right one.
– Occam’s razor
Indeed, much of prior discourse has taken more parameters to mean more complex, leading many to assert that Occam’s razor, while being relevant in the regime of classical statistics, does not apply to over parametrized spaces.
This paper’s fascinating contribution argues instead that simpler solutions are in fact better, and that more successful, highly parameterized neural networks arrive at those simpler solutions because, not despite, their parametrization.
Still, as the authors term it, this is a “conjecture” — it still needs refinement and further investigation. But it’s a well-founded, and certainly interesting, one at that — perhaps with the potential to shift the conversation on how we think about generalization in deep learning.




