Some interesting laws that help you as a Data Scientist
While Data Scientist was working with Data for their main activity, it doesn’t mean that Mathematical knowledge is something we do not need. Data scientists need to learn and understand the mathematical theory behind machine learning to efficiently solving business problems.
The mathematical behind machine learning is not just a random notation thrown here and there, but it consisted of many theories and thoughts. This thought creates a lot of mathematical laws that contributed to the machine learning we able to use right now. Although you could use the mathematical in any way you want to solve the problem, mathematical laws are not limited to machine learning after all.
In this article, I want to outline some of the interesting mathematical laws that could help you as a Data Scientist. Let’s get into it.
Benford’s Law
Benford’s law also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is a mathematical law about the leading digit number in a real-world dataset.
When we think about the first digit of the numbers, it should be distributed uniformly when we randomly took a number. Intuitively, the random number leading digit 1 should have the same probability as leading digit 9, which is ~11.1%. Surprisingly, this is not what happens.
Benford’s law states that the leading digit is likely to be small in many naturally occurring collections of numbers. Leading digit 1 happens more often than 2, leading digit 2 occurs more often than 3, and so on.
Let’s try using a real-world dataset to see how this law is applicable. For this article, I would use the data from Kaggle regarding Spotify Track song from 1921–2020. From the data, I would take the leading digit of the song durations.
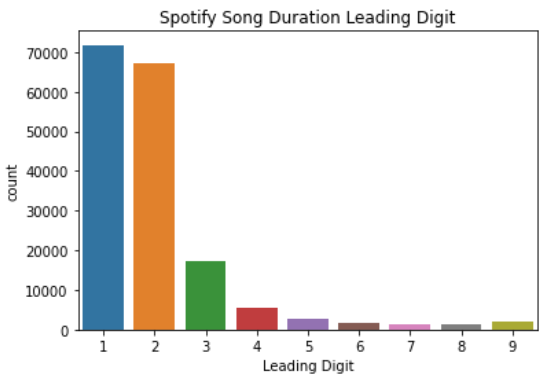
From the image above, we can see that the leading digit 1 occurs the most, then it is decreasing following the higher number. This is what Benford’s Law state above.
If we talk about the proper definition, Benford law state that a set of numbers is said to satisfy Benford’s law if the leading digit d ( ∈1,…,9) occurs with the equation.
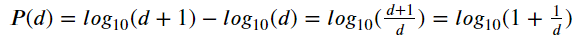
From this equation, we acquired the leading digit with the following distribution.
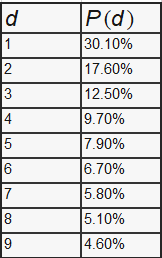
With this distribution, we can predict that 1 as the leading digit is 30% likely to occurs more than the other leading digit.
Many applications for this law, for example, fraud detection on tax forms, election results, economic numbers, and accounting figures.
Law of Large Numbers (LLN)
The Law of Large Number stated that as the number of trials of a random process increases, the results’ average would get closer to the expected values or theoretical values.
For example, when rolling the dice. The possibility of 6-side dice is 1,2,3,4,5 and 6. The mean for the 6-side dice would be 3.5. As we are rolling the dice, the number we get would be random from 1 to 6, but as we keep rolling the dice, the result’s average would get closer to the expected value, which is 3.5. This is what the Law of Large Numbers denote.
While it is useful, the tricky part here is that you need many experiments or occurrences. However, a large number required means that it is good to predict long-term stability.
The Law of Large Numbers is different than the Law of Average, where it was used to express a belief that outcomes of a random event will “even out” within a small sample. This is what we called “Gambler’s Fallacy,” where we expect the expected value would occur in a smaller sample.
Zipf’s Law
Zipf’s law was created for quantitative linguistic, which states that given some natural language dataset corpus, any word’s frequency is inversely proportional to its frequency table rank. Thus the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word.
For example, in the previous Spotify dataset, I would try to split all the words and punctuation to count them. Below is the top 12 of the most common words and their frequency.

When I sum all the word that exists in the Spotify corpus, the total is 759389. We could see if Zipf’s law applies to this dataset by counting the probability when they occur. The first most occurring word or punctuation is ‘-’ with 32258, which has the probability of ~4% then followed by ‘the,’ which has the probability of ~2%.
Faithful to the law, the probability would keep going down in some of the words. Of course, there is a little deviation, but the probability would go down most of the time following the frequency rank increase.
Conclusion
These are some interesting mathematical laws to know as a Data Scientist and definitely would help you in your Data Science work. The laws are:
- Benford’s Law
- Law of Large Number
- Zipf’s Law
I hope it helps!




