This article appeared in Towads Data Science
An overview of the architecture and the implementation details of the most important Deep Learning algorithms for Time Series Classification
Why Time Series Classification?
First of all it’s important to underline why this problem is so important today, and therefore why it is very interesting to understand the role and the potential of Deep Learning in this sector.
During the last years, Time Series Classification has become one of the most challenging problems in Data Science. This has happened because any classification problem that uses data keeping in consideration some notion of sorting, can be treated as a Time Series Classification problem.
Time series are present in many real-world applications ranging from health care, human activity recognition, cyber-security, finance, marketing, automated disease detection, anomaly detection, etc. As the availability of temporal data has increased significantly in the last years, many areas are becoming strongly interested in applications based on time series, and then many new algorithms have been proposed.
All these algorithms, apart from those based on deep learning, require some kind of feature engineering as a separate task before the classification is performed, and this can imply the loss of some information and the increase of the development time. On the contrary, deep learning models already incorporate this kind of feature engineering internally, optimizing it and eliminating the need to do it manually. Therefore they are able to extract information from the time series in a faster, more direct, and more complete way.
Applications
Let’s see some important applications of Reinforcement Learning.
Electrocardiogram records can be used to find out various heart problems, and are saved in time series form. Distinguishing the electrocardiogram of a normal heart from the one of a heart with a disease, and recognizing the disease, is a Time Series Classification problem.
Today many devices can be controlled with the use of simple gestures, without physically touching them. For this purpose these devices record a series of images that are used to interpret the user’s gestures. Identifying the correct gesture from this sequence of images is a Time Series
Classification problem. Anomaly detection is the identification of unusual events or observations which are significantly different from the majority of the data.
Often the data in anomaly detection are time series, for example the temporal trend of a magnitude related to an electronic device, monitored to check that the device is working correctly. Distinguishing the time series of normal operations from that of a device with some anomaly, and recognizing the anomaly, is a Time Series Classification problem.
Problem definition
Now we give a formal definition of a Time Series Classification problem. Suppose to have a set of objects with the same structure (for example real values, vectors or matrices with same size, etc.), and a fixed set of different classes. We define a dataset as a collection of pairs (object, class), which means that to each object is associated a determinate class. Given a dataset, a Classification problem is building a model that associates to a new object, with the same structure of the others, the probability to belong to the possible classes, accordingly to the features of the objects associated to each class.
An univariate time series is an ordered set of real values, while a M dimensional multivariate time series consists of M different univariate time series with the same length. A Time Series Classification problem is a Classification problem where the objects of the dataset are univariate or multivariate time series.
Perceptron (Neuron)
Before introducing the different types of Deep Learning Architectures, we recall some basic structures that they use. First of all we introduce the Perceptron, that is the basic element of many machine learning algorithms. It is inspired by the functionality of biological neural circuits, and for this reason is also called neuron.
This Figure shows the architecture of a Perceptron. A Perceptron has one or more input values, and every input value is associated to a weight.
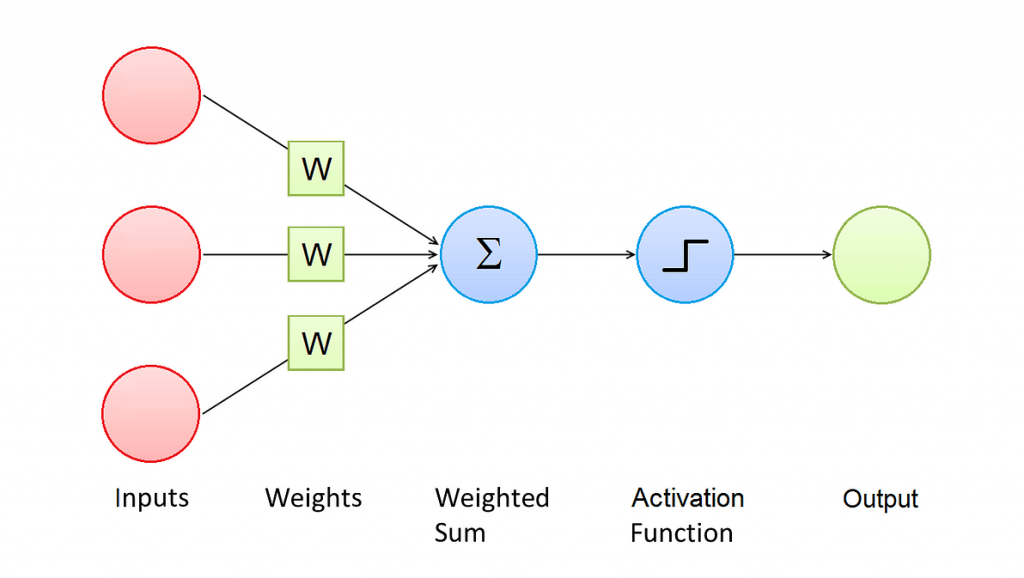
The result of the activation function is referred as the activation of the Perceptron and represents its output value.
Multi Layer Perceptron
Now we introduce the Multi Layer Perceptron (MLP), that is a building block used in many Deep Learning Architectures for Time Series Classification. It is a class of feedforward neural networks and consists of several layers of nodes: one input layer, one or more hidden layers, and one output layer. Every node is connected to all the nodes of its layer, of the previous layer and of the next layer. For this reason we say that Multi Layer Perceptron is fully connected. Each node of the hidden layers and of the output layer is a Perceptron.
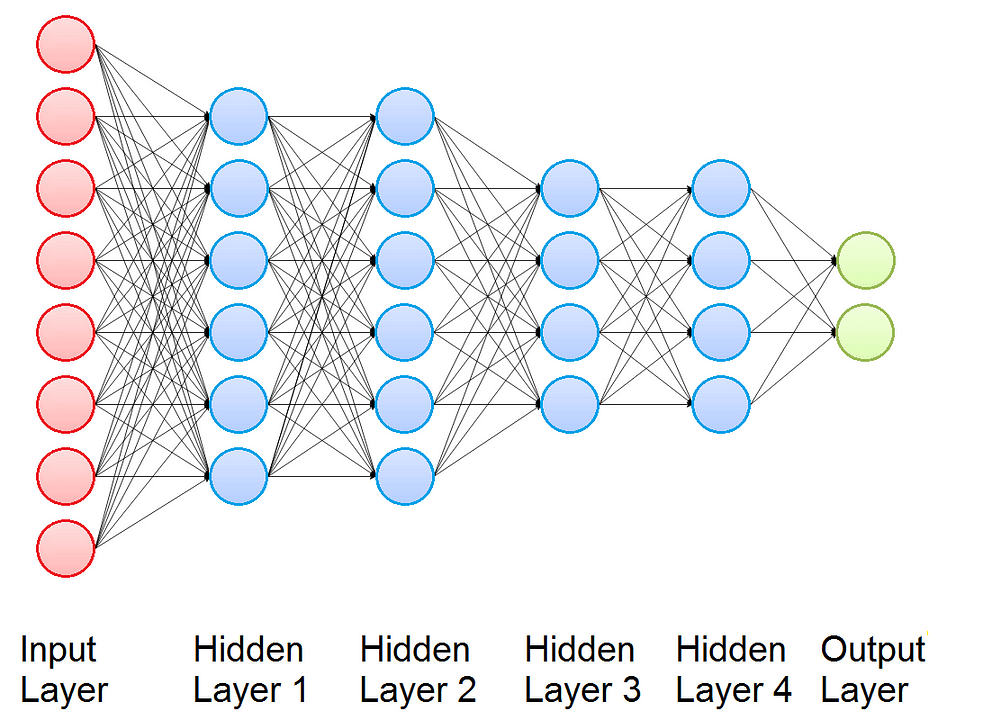
The output of the Multi Layer Perceptron is obtained computing in sequence the activation of its Perceptrons, and the function that connect the input and the output depends on the values of the weights.
Classification with Multi Layer Perceptron
Multi Layer Perceptron is commonly used for Classification problems: given a dataset (that we recall to be a collection of pairs (object, class)), it can be fitted to compute the probability of any new object to belong to each possible class. To do this, first of all we need to represent the pairs (object, class) in the dataset in a more suitable way:
- Every object must be flattened and then represented with a vector, that will be the input vector for training.
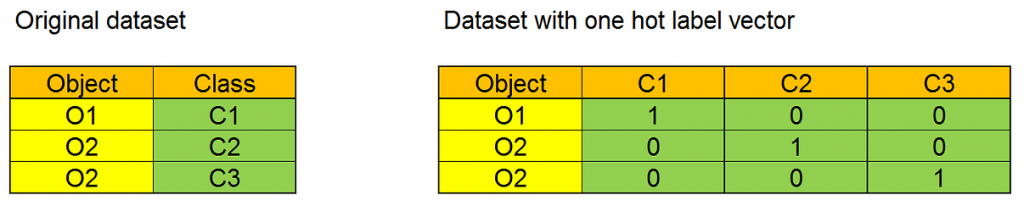
- Every class in the dataset must be represented with its one-hot label vector. A one-hot label vector is a vector with size equal to the number of different classes in the dataset. Each element of the array corresponds to a possible class, and every value is 0 apart from that related to the represented class, that is 1. The one-hot label vector will be the target for training. We can see a simple exampe of one hot label vector in this Figure: in the original dataset the column Class has three different values, and the dataset with the one hot label vector has three columns, one for each class.
In this way we obtain a new dataset of pairs (input vector, target), and we are ready for training. For this process, MLP uses a supervised learning technique called Backpropagation, that works iterating on the input vectors of the dataset:
- At every iteration, the output of the Mlp is computed using the present input vector.
- The output is a vector whose components are the estimated probabilities of belonging to each class.
- The model’s prediction error is computed using a cost function.
- Then, using gradient descent, the weights are updated in a backward pass to propagate the error.
Now, the natural question is: why don’t use the Multi Layer Perceptron for Time Series Classification, taking the whole multivariate time series as input? The answer is that Multi Layer Perceptron, as many other Machine Learning algorithms, don’t work well for Time Series Classification because the length of the time series really hurts the computational speed. Hence, to obtain good results for Time Series Classification it is necessary to extract the relevant features of the input time series, and use them as input of a classification algorithm, in order to obtain better results in a very lower computation time.
The big advantage of Deep Learning algorithms with respect to other algorithms is that these relevant feature are learned during the training, and not handcrafted. This improves very much the accuracy of the results and makes the data preparation time much lower. Then, after many layers used for the extraction of these relevant features, many Deep Learning architecures can use algorithms like MLP to obtain the desired classification.
Deep Learning for Time Series Classification
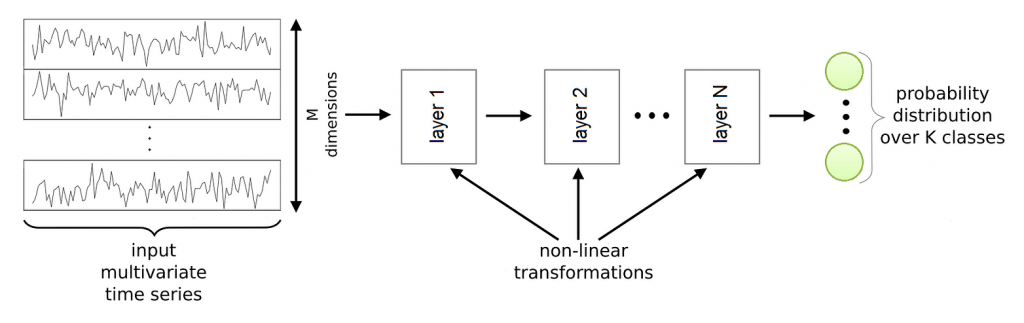
This Figure shows a general Deep Learning framework for Time Series Classification. It is a composition of several layers that implement non-linear functions. The input is a multivariate time series. Every layer takes as input the output of the previous layer and applies its non-linear transformation to compute its own output.
The behavior of these non-linear transformations is controlled by a set of parameters for each layer. These parameters link the input of the layer to its output, and are trainable (like the weights of the Multi Layer Perceptron). Often, the last layer is a Multi Layer Perceptron or a Ridge regressor.
In this artitcle 3 different Deep Learning Architecture for Time Series Classifications are presented:
- Convolutional Neural Networks, that are the most classical and used architecture for Time Series Classifications problems
- Inception Time, that is a new architecure based on Convolutional Neural Networks
- Echo State Networks, that are another recent architecure, based on Recurrent Neural Networks
Convolutional Neural Networks
A Convolutional Neural Network is a Deep Learning algorithm that takes as input an image or a multivariate time series, is able to successfully capture the spatial and temporal patterns through the application trainable filters, and assigns importance to these patterns using trainable weights. The pre processing required in a Convolutional Neural Network is much lower as compared to other classification algorithms. While in many methods filters are hand-engineered, Convolutional Neural Network have the ability to learn these filters.
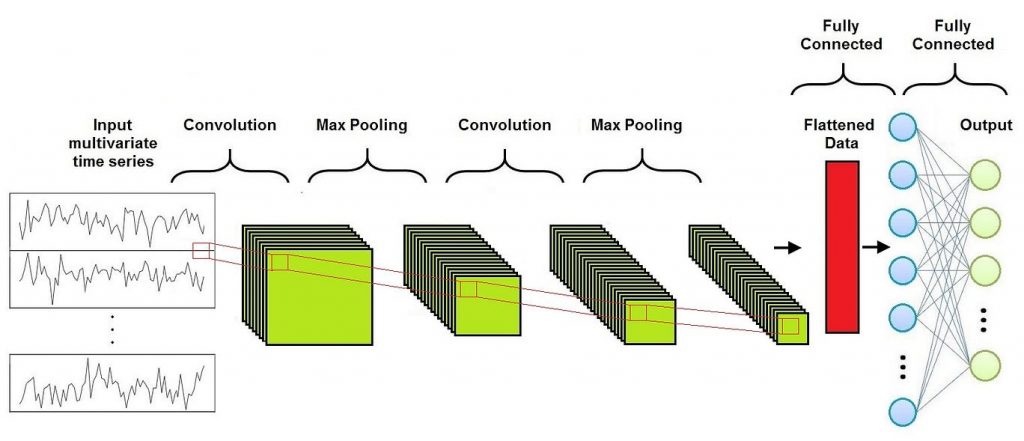
As we can see in this Figure, a Convolutional Neural Network is composed of three different layers:
- Convolutional Layer
- Pooling Layer
- Fully-Connected Layer
Usually several Convolutional Layers and Pooling Layers are alternated before the Fully-Connected Layer.
Convolutional Layer
The convolution operation gives its name to the Convolutional Neural Networks because it’s the fundamental building block of this type of network. It performs a convolution of an input series of feature maps with a filter matrix to obtain as output a different series of feature maps, with the goal to extract the high-level features.
The convolution is defined by a set of filters, that are fixed size matrices. When a filter is applied to a submatrix of the input feature map with its same size, the result is given by the sum of the product of every element of the filter with the element in the same position of the submatrix (we can see this in this Figure).
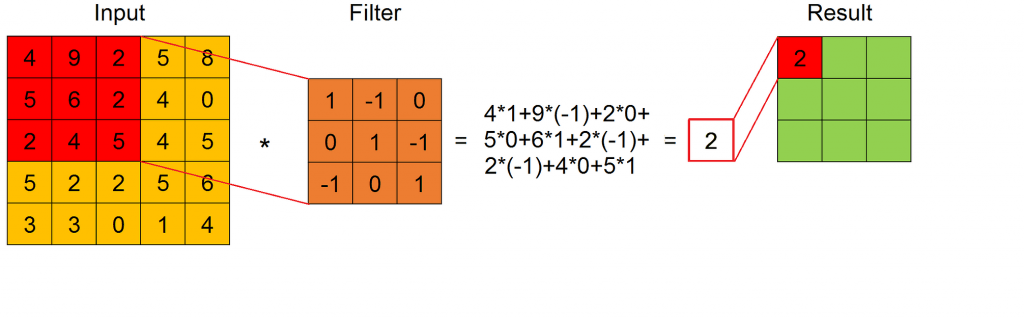
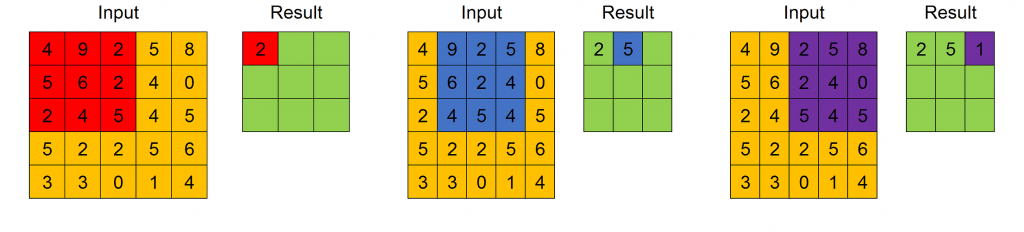
The result of the convolution between one input feature map and one filter is the ordered feature map obtained applying the filter across the width and height of the input feature map, as in this Figure.
A Convolutional Layer executes the convolution between every filter and every input feature map, obtaining as output a series of features maps. As already underlined, the values of the filters are considered as trainable weights and then are learned during training.
Two important parameters that must be chosen for the Convolutional Layer are stride and padding.
Stride
Stride controls how the filter convolves around one input feature map. In particular, the value of stride indicates how many units must be shifted at a time, how we can see in this Figure.
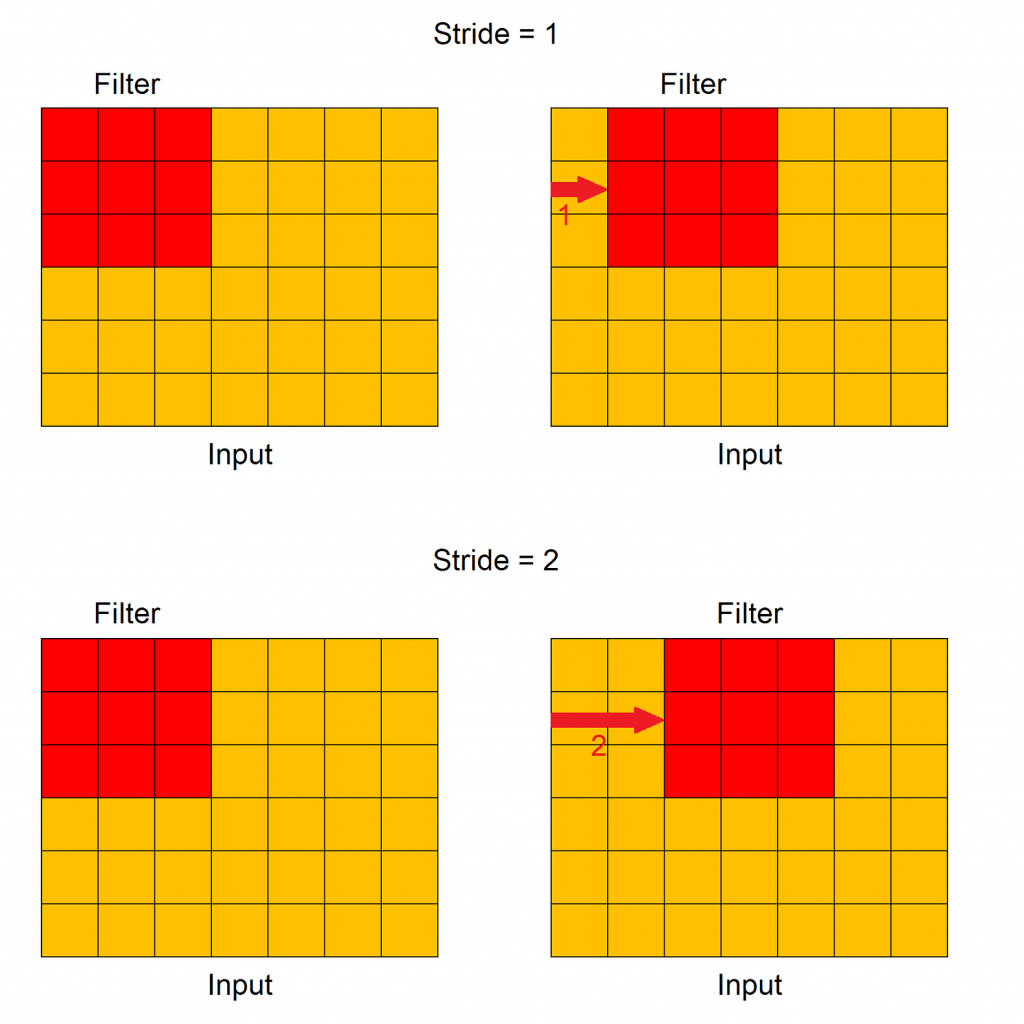
Padding
Padding indicates how many extra columns and rows to add outside an input feature map, before applying a convolution filter, how we can see in this Figure. All the cells of the new columns and rows have a dummy value, usually 0.
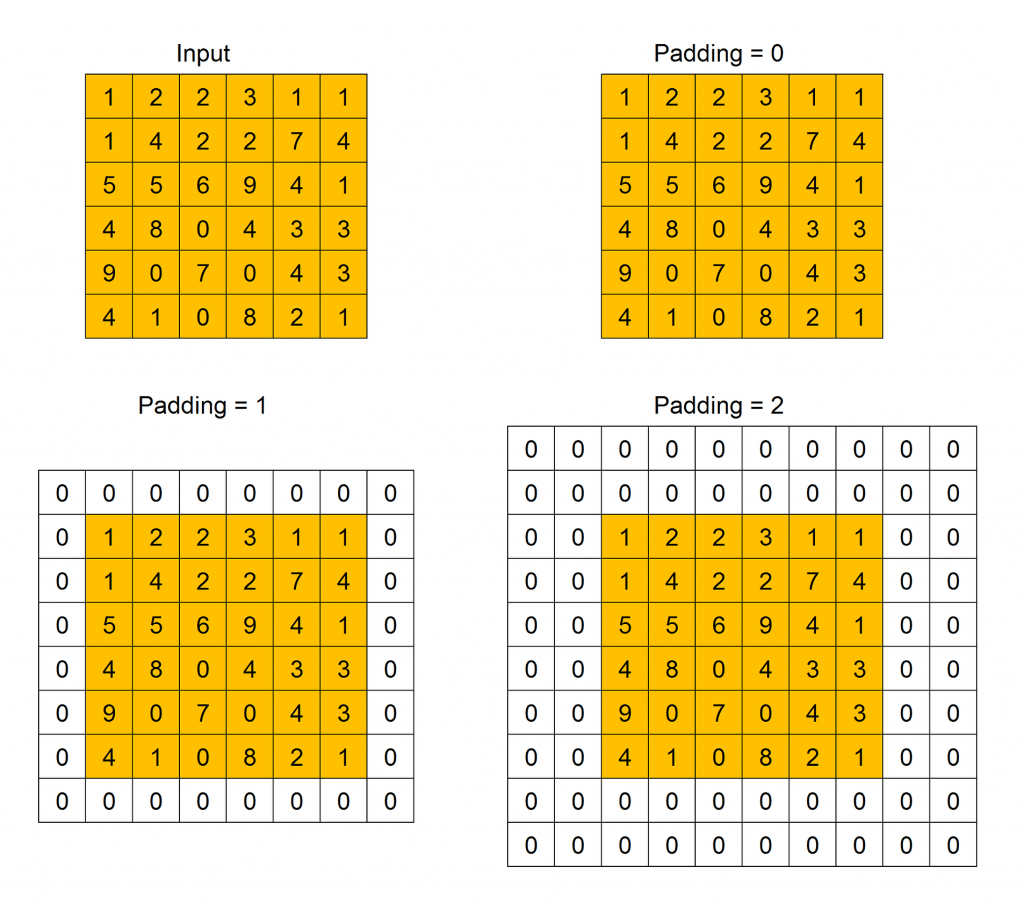
Padding is used because when a convolution filter is applied to an input feature map, its size decreases. Then, after the application of many filter the size can become too small. Adding extra rows and columns we can preserve the original size, or make it decreasing slower.
When the size of the feature map obtained after the application of the convolution filter is smaller than the size of the input feature map, we call this operation Valid Padding. When the output size is equal or grater of the input size, we call this operation Same Padding.
Pooling Layer
The purpose of pooling operation is to achieve a dimension reduction of feature maps, preserving as much information as possible. It is useful also for extracting dominant features which are rotational and positional invariant. Its input is a series of feature maps and its output is a different series of feature maps, with lower dimension.
Pooling is applied to sliding windows of fixed size across the width and height of every input feature map. There are two types of pooling: Max Pooling and Average Pooling. As we can see in the Figure, for every sliding window the result of the pooling operation is its maximum value or its average value, respectively for Max Pooling or Average Pooling.
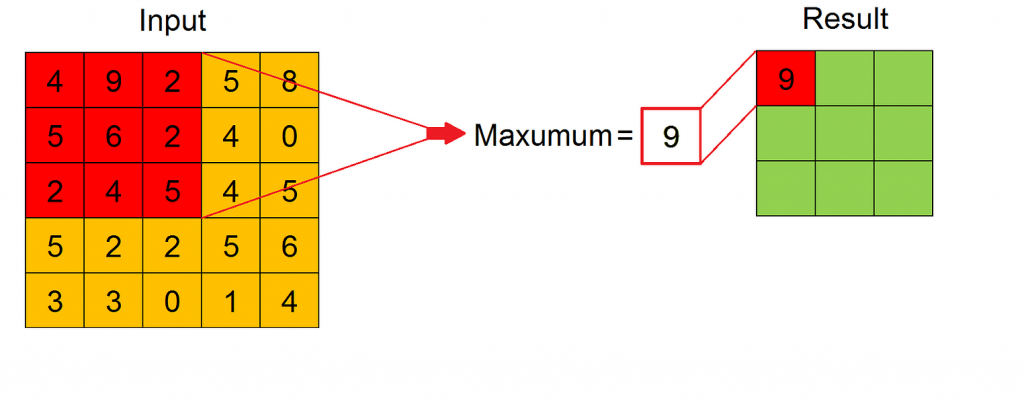
Max Pooling works also as a noise suppressant, discarding noisy activations altogether. Hence, it usually performs better than Average Pooling. Also for Pooling Layer stride and padding must be specified.
The advantage of pooling operation is down-sampling the convolutional output bands, thus reducing variability in the hidden activations.
Fully-Connected Layer
The goal of the Fully-Connected Layer is to learn non-linear combinations of the high-level features represented by the output of the Convolutional Layer and the Pooling Layer. Usually the Fully Connected Layer is implemented with a Multi Layer Perceptron.
After several convolution and pooling operations, the original time series is represented by a series of feature maps. All these feature maps are flattened into a column vector, that is the final representation of the original input multivariate time series. The flattened column is connected to the Multi-Layer Perceptron, whose output has a number of neurons equal to the number of possible classes of time series.
Backpropagation is applied to every iteration of training. Over a series of epochs, the model is able to distinguish the input time series thanks to their dominant high-level features and to classify them.
Hyperparameters
For Convolutional Neural Networks neural network there are numerous hyperparameters to specify. The most important are the following:
- Number of convolution filters – Obviously too few filters cannot extract enough features to achieve classification. However, more filters are helpless when the filters are already enough to represent the relevant features, and make the training more computationally expensive.
- Convolution filter size and initial values – Smaller filters collect as much local information as possible, bigger filters represent more global, high level and representative information. The filters are usually initialized with random values.
- Pooling method and size – As already mentioned, there are two types of pooling: Max Pooling and Average Pooling, and Max Pooling usually performs better since it works also as noise suppressant. Also the pooling size is an important parameter to be optimized, since if the the pooling size increases, the dimension reduction is greater, but more informations are lost.
- Weight initialization – The weights are usually initialized with small random numbers to prevent dead neurons, but not too small to avoid zero gradient. Uniform distribution usually works well.
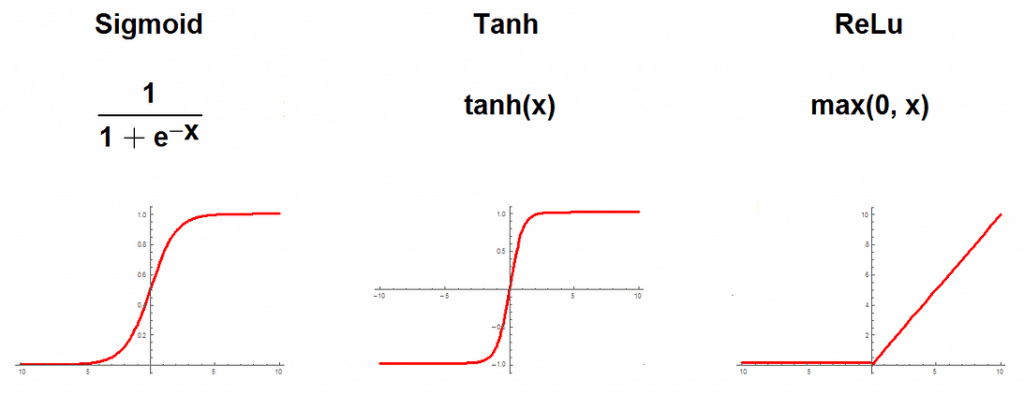
- Activation function – Activation function introduces non-linearity to the model. Rectifier, sigmoid or hyperbolic tangent are usually chosen.
- Number of epochs – Number of epochs is the the number of times the entire training set pass through the model. This number should be increased until there is a small gap between the test error and the training error, if the computational performances allow it.
Implementation
Building a Convolutional Neural Network is very easy using Keras. Keras is a simple-to-use but powerful deep learning library for Python. To build a Convolutional Neural Network in Keras are sufficient few steps:
- First of all, declare a Sequential class; every Keras model is either built using the Sequential class, which represents a linear stack of layers, or the Model class, which is more flexible. Since a CNN is a linear stack of layers, we can use the simpler Sequential class;
- Add the desired Convolutional, MaxPooling and Dense Keras Layers in the Sequential class;
- Specify number of filters and filter size for Convolutional Layer;
- Specify pooling size for Pooling Layer.
To compile the model, Keras needs more informations, that are:
- input shape (once that the input shape is specified, Keras automatically infers theshapes of inputs for later layers);
- optimizer (for example Stochastic gradient descent or Adagrad);
- loss function (for example mean squared error or mean absolute percentage error);
- list of metrics (for example accuracy).
Training a model in Keras literally consists only of calling function fit() specifying the needed parameters, that are:
- training data (input data and labels),
- number of epochs (iterations over the entire dataset) to train for,
- validation data, which is used during training to periodically measure the network’s performance against data it hasn’t seen before.
Using the trained model to make predictions is easy: we pass an array of inputs to the function predict() and it returns an array of outputs.
Inception Time
Recently was introduced a deep Convolutional Neural Network called Inception Time. This kind of network shows high accuracy and very good scalability.
Inception Network Architecture
The Architecture of an Inception Network is similar to the one of a Convolutional Neural Network, with the difference that Convolutional Layers and Pooling Layers are replaced with Inception Modules.
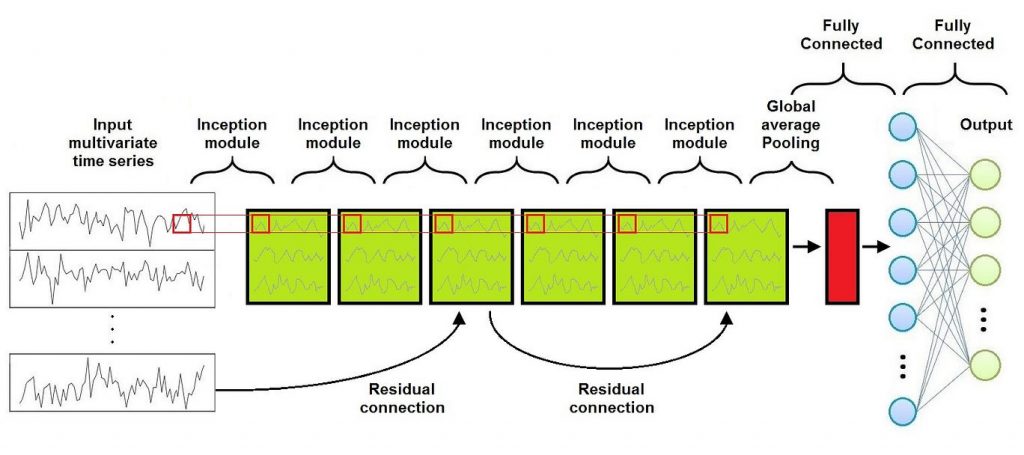
As shown in this Figure, the Inception Network consists of a series of Inception Modules followed by a Global Average Pooling Layer and a Fully Conencted Layer (usually a Multi Layer Perceptron). Moreover, a residual connections is added at every third inception module. Each residual block’s input is transferred via a shortcut linear connection to be added to the next block’s input, thus mitigating the vanishing gradient problem by allowing a direct flow of the gradient.
Inception Module
The major building block of an Inception Network is the Inception Module, shown in this Figure.
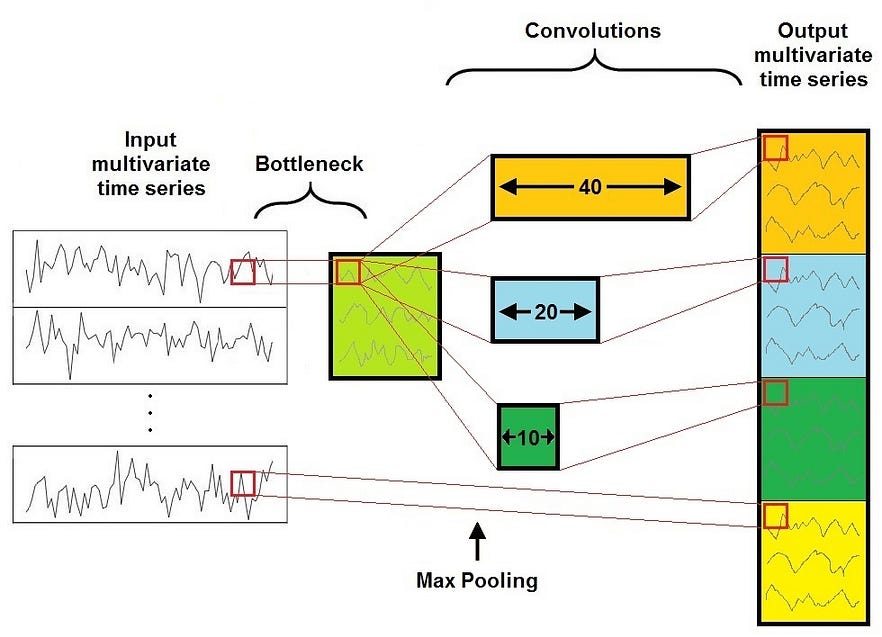
It consists of 4 Layers:
- The first layer is a bottleneck layer, that reduces the dimensionality of the inputs. This reduces also the computational cost and the number of parameters, speeding up training and improving generalization.
- The second major component of the Inception Module is a set of parallel Convolutional Layers of different size acting on the same input feature map. For example in the Figure there are three different convolutions with filter size 10, 20, and 40.
- The third layer is a MaxPooling, that introduces the ability of having a model that is invariant to small perturbations.
- The fourth and last layer is a Depth Concatenation Layer, where the output of each independent parallel convolution and of the MaxPooling is concatenated to form the output multivariate time series of the current Inception Module.
By stacking multiple Inception Modules and training the filters’ values via backpropagation, the network is able to extract latent hierarchical features of multiple resolutions thanks to the use of filters with different sizes. This is the big advantage of the Inception Module since it allows the internal layers to pick and choose which filter size is relevant to learn the required information. This is very helpful to identify a high-level feature that can have different sizes on different input feature maps.
Receptive Field
The key parameter to understand an Inception Network is its Receptive Field. Unlike fully-connected networks, a neuron in an Inception Network depends only on a region of the input features map. This region is called Receptive Field of the neuron. Clearly, bottom-layer neurons depend on regions that are smaller than those of top-layer. Then, bottom-layer neurons are expected to capture the local structure of a time series, while the top-layer neurons are expected to identify more complex patterns.
For time series data, the total Receptive field of an Inception Network is defined from this formula, that depends only on the length of the filters k_i and on depth of the network d (that is the number of Inception Modules):
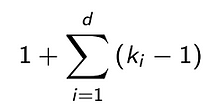
It’s very interesting to investigate how the accuracy of an Inception Network changes as the Receptive Field varies. To vary the Receptive Field we can change the filter lengths or the depth of the network.
In most cases a longer filter is required to produce more accurate results. This is explained by the fact that longer filters are able to capture longer patterns with higher probability than shorter ones. On the contrary, increasing the Receptive Field by adding more layers doesn’t necessarily give an improvement of the network’s performance, especially for datasets with a small training set. Hence in order to improve accuracy it’s usually better to increase the filter lengths instead of adding more layers.
Inception Time Architecture
Many experiments have shown that a single Inception Network sometimes exhibits high variance in accuracy. This is probably because of the variability given by the random weights initialization.
In order to overcome this instability, generally Inception Time is implemented as an ensemble of many Inception Networks, and every prediction has the same weight. In this way the algorithm improves his stability, and shows the already mentioned high accuracy and very good scalability.
In particular different experiments have shown that its time complexity grows linearly with both the training set size and the time series length, and this is a very good result since many other algorithms grow quadratically with respect to the same magnitudes.
Implementation
A full implementation of Inception Time can be found on GitHub (https://github.com/hfawaz/InceptionTime). The implementation is written in Python and uses Keras. This implementation is based on 3 main files:
- file main.py contains the necessary code to run an experiement;
- file inception.py contains the Inception Network implementation;
- file nne.py contains the code that ensembles a set of Inception Networks.
In particular, the implementation uses the already mentioned Keras Module Class, since some layers of InceptionTime work in parallel, unlike Convolutional Neural Networks that uses Sequential Class since their layers are all in series.
The code that implements the Inception Module building block is very similar to that described for Convolutional Neural Networks, since it uses Keras Layers for Convolution and MaxPooling, and hence it can be easily used or included in codes based on Keras in order to implement customized architectures.
Recurrent Neural Networks
Echo State Networks are a type of Recurrent Neural Networks, hence it can be useful a small introduction about them. Recurrent Neural Networks are networks of neuron-like nodes organized into successive layers, with an architecture similar to the one of standard Neural Networks. Infact, like in standard Neural Networks, neurons are divided in input layer, hidden layers and output layer. Each connection between neurons has a corresponding trainable weight.
The difference is that in this case every neurons is assigned to a fixed timestep. The neurons in the hidden layer are also forwarded in a time dependent direction, that means that everyone of them is fully connected only with the neurons in the hidden layer with the same assigned timestep, and is connected with a one-way connection to every neuron assigned to the next timestep. The input and output neurons are connected only to the hidden layers with the same assigned timestep.
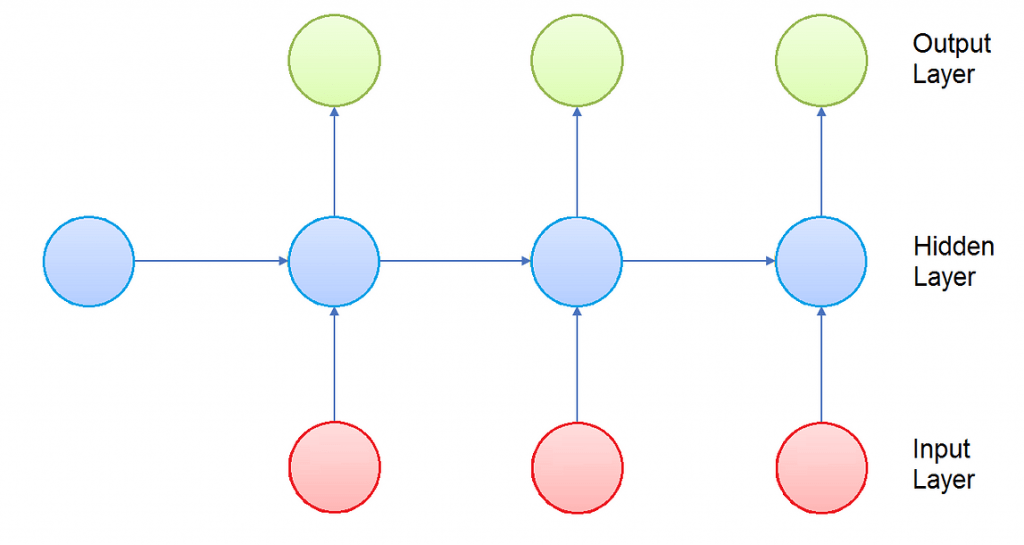
Since the output of the hidden layer of one timestep is part of the input of the next timestep, the activation of the neurons is computed in time order: at any given timestep, only the neurons assigned to that timestep computes their activation.
Recurrent Neural Networks are rarely applied for Time Series Classification mainly due to three factors:
- The type of this architecture is designed mainly to predict an output for each element in the time series.
- When trained on long time series, Recurrent Neural Networks typically suffer from the vanishing gradient problem, that means that the parameters in the hidden layers either don’t change that much or they lead to numeric instability and chaotic behavior.
- The training of a Recurrent Neural Network is hard to parallelize, and is also computationally expensive.
Echo State Networks were designed to mitigate the problems of Recurrent Neural Networks by eliminating the need to compute the gradient for the hidden layers, reducing the training time and avoiding the vanishing gradient problem. Infact many results show that Echo State Networks are really helpful to handle chaotic time series.
Echo State Networks
As shown in the Figure, the Architecture of an Echo State Network consists of an Input Layer, a hidden Layer called Reservoir, a Dimension Reduction Layer, a Fully Connected Layer called Readout, and an Output Layer.
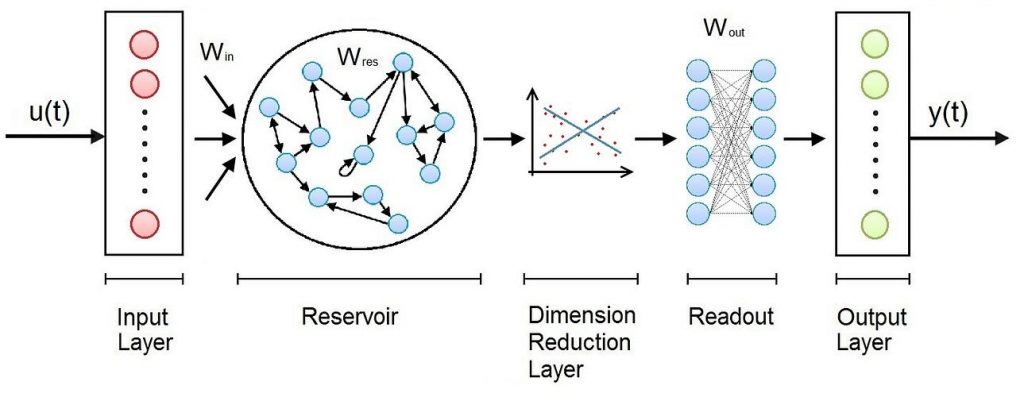
- The Reservoir is the main building block of an Echo State Network and is organized like a sparsely connected random Recurrent Neural Network.
- The Dimension Reduction algorithm is usually implemented with the Principal Component Analysis.
- The Readout is usually implemented as Multi Layer Perceptron or a Ridge regressor.
The weights between the Input layer and the Reservoir and those in the Reservoir are randomly assigned and not trainable. The weights in the Readout are trainable, so that the network can learn and reproduce specific patterns.
Reservoir
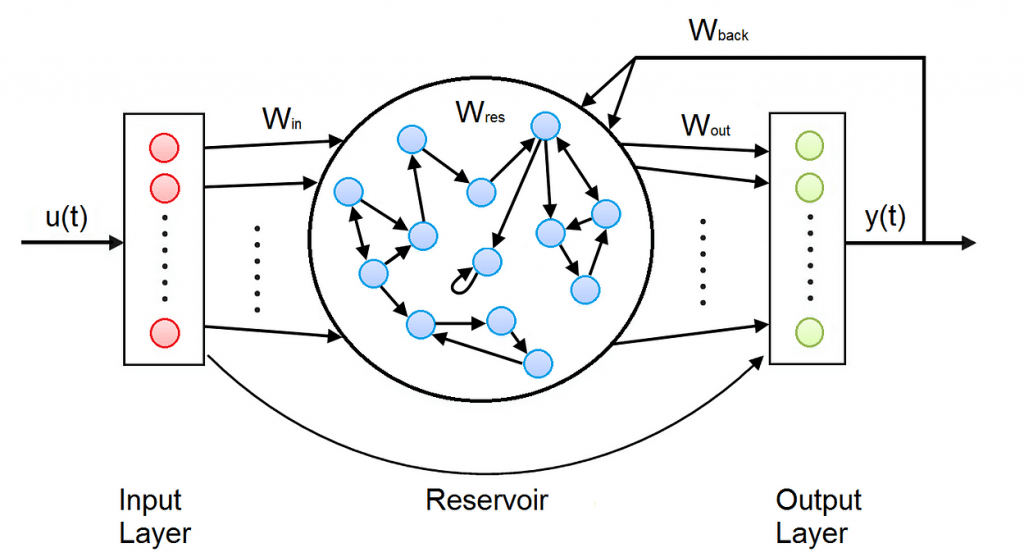
As already mentioned, the Reservoir is organized like a sparsely connected random Recurrent Neural Network. The Reservoir is connected to the Input Layer, and consists in a set of internal sparsely-connected neurons, and in its own output neurons. In the Reservoir there are 4 types of weights:
- input weights between the Input Layer and the internal neurons;
- internal weights, that connect the internal neurons to each other;
- output weights between the internal neurons and the output;
- backpropagation weights, that connect back the output to the internal neurons. All these weights are randomly initialized, are equal for every time step and are not trainable.
Like in RNNs, the output of the Reservoir is computed separately for every time step since the output of a time step is part of the input of the next time step. At every time step, the activation of every internal and output neuron is computed, and the output for the current timestep is obtained.
The big advantage of ESNs is that the Reservoir creates a recurrent non linear embedding of the input into a higher dimension representation, but since only the weights in the Readout are trainable, the training computation time remains low.
Dimension Reduction
Many experiments show that choosing the correct dimension reduction it’s possible to reduce the execution time without lowering the accuracy. Moreover dimensional reduction provides a regularization that improves the overall generalization capability and robustness of the models.
In most cases the training time increases almost linearly with the subspace dimension, while the accuracy quickly increases as long as the subspace dimension is below a certain threshold, then after this threshold it slows down strongly and remains almost constant. Hence this threshold is the best choice for the subspace dimension since with a higher value we would have a longer execution time without relevant improvements in the accuracy.
Implementation
A full implementation in Python of Echo State Networks is available on GitHub (https://github.com/FilippoMB/Reservoir-Computing-framework-for-multivariate-time-series-classification). The code uses the libraries Scikit-learn and SciPy. The main class RC_classifier contained in the file modules . py permits to build, train and test a Reservoir Computing classifier, that is the family of algorithms to which the Echo State Networks belong.
The hyperparameters requested for the Reservoir must be optimized in order to obtain the desired accuracy and the desired performance for the execution time; the most important are:
- the number of neurons in the Reservoir;
- the percentage of nonzero connection weights (usually less then 10%);
- the largest eigenvalue of the reservoir matrix of connection weights.
The most important hyperparameters in other layers are:
- the algorithm for Dimensional Reduction Layer (that can be None or tensorial PCA for multivariate time series data);
- the subspace dimension after the Dimension Reduction Layer;
- the type of Readout used for classification (Multi Layer Perceptron, Ridge regression, or SVM);
- the number of epochs, that is the number iterations during the optimization.
The structure of the code that implements training and uses of the model is very similar to that described for Convolutional Neural Networks.
Conclusions
Convolutional Neural Networks are the most popular Deep Learning technique for Time Series Classifications, since they are able to successfully capture the spatial and temporal patterns through the use of trainable filters, assigning importance to these patterns using trainable weights.
The main difficulty in using CNNs is that they are very dependent on the size and quality of the training data. In particular, the length of the time series can slow down training, and results can be not accurate as expected with chaotic input time series or with input time series in which the same relevant feature can have different sizes. To solve this problems, many new algorithms were recently elaborated, and among these InceptionTime and Echo State Networks perform better than the others.
InceptionTime is derived from Convolution Neural Networks and speeds up the training process using an efficient dimension reduction in the most important building block, the Inception Module. Moreover it performs really well in handling input time series in which the same relevant feature can have different sizes.
Echo State Networks are based on Recurrent Neural Networks, and speed up the training process because they are very sparsely connected, with most of their weights fixed a priori to randomly chosen values. Thanks to this, they demonstrate remarkable performances after very fast training. Moreover they are really helpful to handle chaotic time series.
Hence, in conclusion, high accuracy and high scalability make these new architectures the perfect candidate for product development.
References
- Hassan Ismail Fawaz, Benjamin Lucas, Germain Forestier, Charlotte Pelletier, Daniel F. Schmidt, Jonathan Weber, Geoffrey I. Webb, Lhassane Idoumghar, Pierre-Alain Muller, François Petitjean. InceptionTime: Finding AlexNet for Time Series Classification.
- Filippo Maria Bianchi, Simone Scardapane, Sigurd Løkse, Robert Jenssen. Reservoir computing approaches for representation and classification of multivariate time series.




