good model loss ≠ good learning
All machine learning models originate in the computer lab. They’re initialized, trained, tested, redesigned, trained again, fine-tuned, tested yet again before they are deployed.
Afterwards, they fulfill their duty in epidemiological modelling, stock trading, shopping item recommendation, and cyber attack detection, among many other purposes. Unfortunately, success in the lab may not always mean success in the real world — even if the model does well on the test data.
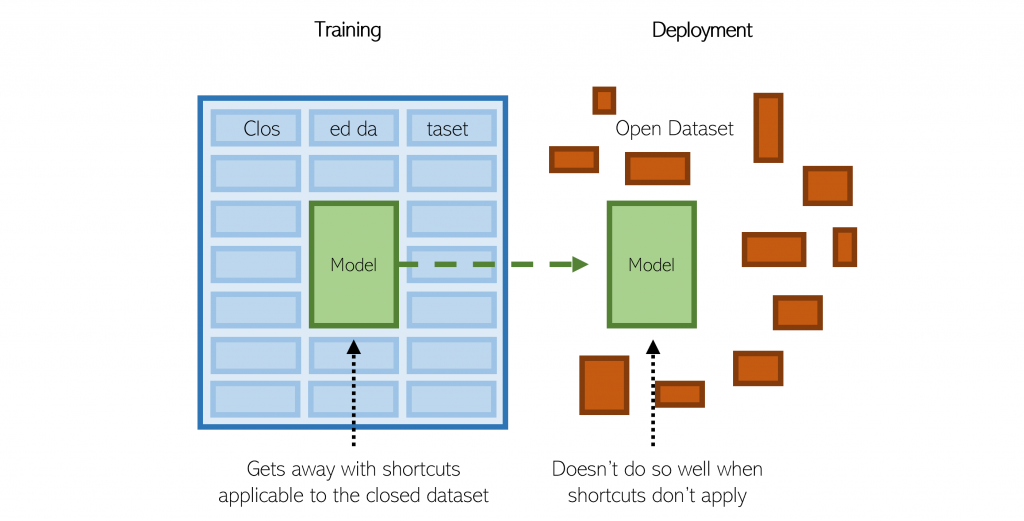
This big problem — that the machine learning models being developed on the computer to serve a purpose in the real world can often crash — has had little research or discussion. Usually, the solution is to assume that the data given to the model was not representative, or something similar.
A valid solution as that may be, recently in November of 2020 a group of several researchers proposed a more broad explanation for this phenomenon: underspecification. While underspecification certainly has been explored deeply, the researchers write, “its implications for the gap between iid (model training ‘in the lab’) and application-specific generalization are neglected.”
Take this example — we’re trying to use machine learning to find the future maximum number of birds there will be in an exhibit at the zoo.
The first step is to create a model modelling the number of birds were on the zoo x years since the exhibit opened. The model our algorithm derives is a quartic one, with three extrema. The number of birds in the exhibit steadily rises through reproduction, then suddenly plummets (perhaps a disease).
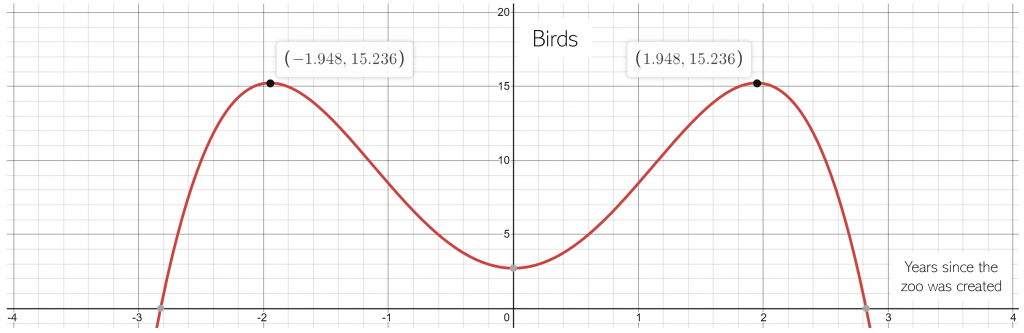
The next step is to find the maximum value of this model we’ve created. We’ll create an optimizer, which initializes at a random point and uses derivatives to find in which direction it should move.
For instance, in this case the initialized optimizer can move left or right: if it moves left, the number of birds goes up; if it moves right, the number of birds goes down. Since the optimizer’s goal is to find the maximum number of birds, it’ll move to the left.
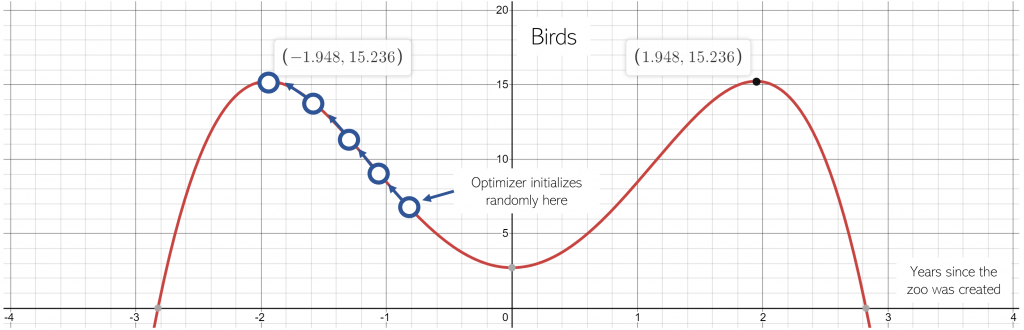
Viola! Our crafty model has found the maximum number of birds there will be in the zoo exhibit will be reached 1.948 years before the exhibit opened.
Obviously, the model has come to a false conclusion. What went wrong?
This is an easy question to answer. We didn’t specify the actual domain of the phenomena we’re trying to model. We should have set some sort of constraint in the code of our model such that the optimizer searches only valid years.
optimizer.find_maximum(search_range="0<=x")
Using this would have made the model we created better model the phenomena of bird population growth (and sudden decline). By specifying these limits, we would be able to eliminate answers that are the product of artificial representations, like an object existing before its creation.
In this case, it’s fairly easy to see that the answer the model spits out is patently wrong, and to slap a limitation on it so it behaves. However, this easiness of fixing the model is accompanied, not by coincidence, with the fact that it can’t really do much. The model takes in one input — the year — and predicts based on a polynomial the population.
What’s harder — a lot more harder — is to do the same thing with massive neural networks, which are the most prone to underspecification. Furthermore, these massive neural networks are often used to model phenomena a lot more complex than birds in a zoo, like the behavior patterns of millions of users or the distinguishing features of thousands of faces.
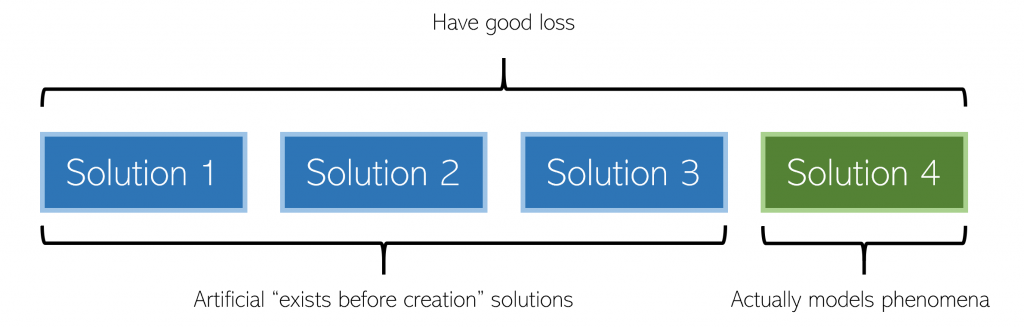
So, we have a problem (usually, finding the best parameters for a neural network), and multiple solutions (combinations of parameters for a neural network). That is, they are parameters that can achieve similarly good loss, both in training and validation.
Underspecification becomes an issue when the problem has only one solution, but the method through which we find solutions yields multiple.
There’s one true solution that models the phenomena desired, but we can’t put specifications on the solution-finding process (because it’s too complicated), so we find multiple that all look great by our metric.
Let’s consider a neural network trained to model the best video to recommend to a user. It takes in inputs about the user’s behavior, and outputs the probability from zero to one that they would enjoy watching a certain video, for tens of thousands of videos. There’s likely only one set of weights that truly captures the thought process of a user as they watch a video, but many weights that can artificially connect input to target quite well.
Think of it as answering 1 + 1 = ?. The natural way is to understand that the notation x + ymeans “add the two numbers” and to answer 2. An artificial way to answer is to say that x + y means (2x)/y. Indeed, this definition satisfies 1+1=2. But it doesn’t capture the phenomena intended, and doesn’t work as well for all situations or variants of the phenomena.
(With something as complex as a massive neural network, it’s not infeasible at all to expect it to dream up as solution as contrived as (2x)/y, even with measures like regularization.)
Other solutions may look good in the lab, because they’re artificial solutions, like the maximum number of birds existing 1.948 years before they were even put in the exhibit. However, when they’re deployed in the real world, they won’t perform as well, because they haven’t actually learned the mechanics of the phenomena as completely as another solution. They might still be parsing (x+y+2)/2 instead of simply adding the two numbers.
Building upon this — any specification is a condition or fixing of parameters. A model with many fixed parameters will have low underspecification. However, large models with many trainable parameters, like deep neural networks, are especially prone to underspecification.
Further, random initialization plays a problem in underspecification. Because there are so many solutions that look good to the optimizer, and the optimizer can’t tell which ones actually measure the phenomenon or not, we can’t really tell if a trained model really does understand the data. Hence, something as arbitrary as a random seed can be the difference in deployment success.
This is why multiple models can be trained and evaluated on the same data and yield the same loss, while performing very different in deployment.
Underspecification occurring in ML pipelines can block the reliability of models that behave as expected in deployment.
Underspecification occurs in many facets of machine learning. The researchers that introduced underspecification in this context ran ‘stress tests’ — probing the output based on a carefully designed input to measure the model’s biases — on a variety of models and contexts.
From genomics to epidemiology, and small neural networks to deep convolutional networks to natural language processing, underspecification applies. This has big implications for how we view learning.
Are natural language processing systems actually learning general linguistic principles like grammar, or are they taking artificial shortcuts? Results of stress tests on these systems, along with a large body of research, cast doubt on the idea that our deepest NLP models are actually learning the language.
There is an interest in creating models that understand the human language if their purpose is to serve humans. A NLP model that relies on linguistic shortcut and not linguistic understanding to perform a task might work nicely in a lab, but as soon as it is deployed it will have trouble.
We’ve always known that machine learning algorithms were lazy, but we haven’t considered them essentially lying to us. Since often phenomena in neural networks is answered with “it’s a black box”, we haven’t explored it to much at all.
Underspecification in this respect is relatively knew, and very important. How to solve it is an important question not only to the practical problem of making model deployment more stable, but how to make models actually learn the mechanics of the data instead of taking shortcuts or generating nonsense artificial solutions.
Going forward, this will become an important idea to investigate and even — perhaps — to solve.
Read the paper that introduced underspecification in relation to model deployment here. If you’re interested in this topic, you may also like some other articles in a similar vein:




