In this post, I argue that the graph isomorphism setting is too limiting for analysing the expressive power of graph neural networks and suggest a broader setting based on metric embeddings.
This is the third in the series of posts on the expressivity of graph neural networks. See Part 1 describing the relation between graph neural networks and the Weisfeiler-Lehman graph isomorphism test, and see Part 2 showing how to construct provably powerful graph neural networks based on substructure counting.
Weisfeiler-Lehman (WL) test [1] is a general name for a hierarchy of graph-theoretical polynomial-time iterative algorithms providing a necessary but insufficient condition for graph isomorphism. In the context of deep learning on graphs, it was shown that message passing neural networks are as powerful as the 1-WL test [2]. Going to higher-order and hence more powerful k-WL tests leads to graph neural networks with high computational complexity and non-local operations [3], which are impractical in real applications.
A different approach, which we introduced in a recent paper [4], is to break from the Weisfeiler-Lehman hierarchy and resort to a message passing mechanism that is aware of local graph structures such as cycles, cliques, and paths. This leads to graph neural networks that have the attractive locality and low-complexity of standard message-passing architectures, at the same time being provably more powerful than 2-WL and at least not less powerful than 3-WL. Such a view opens deep links to open problems in graph theory that have not been previously explored in the context of graph neural network expressivity.
Is this the end of the story? I believe we can do better by changing the perspective on the problem and will discuss a few directions in this post.
Approximate isomorphisms. While important insights into the expressive power of graph neural networks have emerged from the link to the graph isomorphism problem, the setting itself is rather limited. Graph neural networks can be seen as attempting to find a graph embedding f(G), with the desired property f(G)=f(G′) iff G~G′. Unfortunately, since the Weisfeiler-Lehman test is a necessary but not sufficient condition for graph isomorphism, this works only one way: f(G)=f(G′) if G~G′, but the converse is not necessarily true: two non-isomorphic graphs can result in equal embeddings.
In practical applications, we rarely deal with exactly isomorphic graphs but rather graphs that are approximately isomorphic, as shown in the following figure:
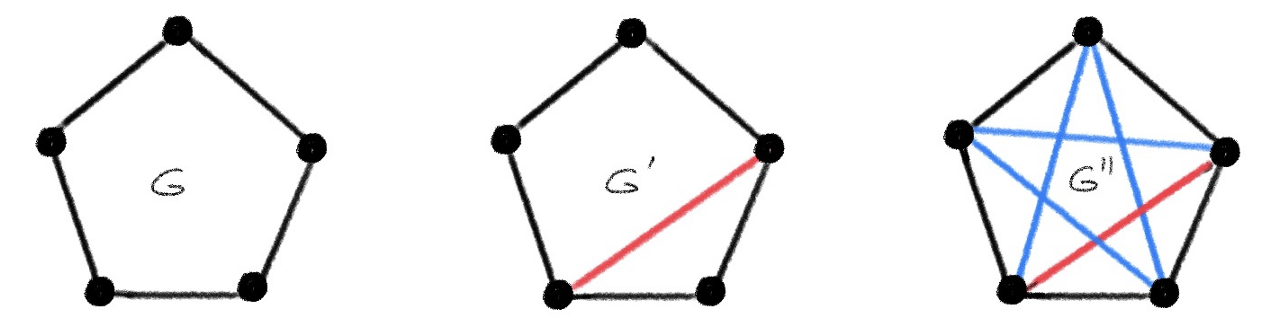
A proper way of quantifying the notion of “approximate isomorphism” is in the form of a metric d, which is large if the two graphs are dissimilar and small otherwise. Graph edit distance [5] or the Gromov-Hausdorff distance [6] are two possible examples. Importantly, the metric is defined to be d(G,G′)=0 iff G~G′ , implying that two isomorphic graphs are indiscernible [7]. The problem of isometric embedding
|f(G)−f(G′)|=d(G,G′) for all G, G′ (♠)
attempts to replace the graph distance with the Euclidean distance |.| between the embeddings of the graphs in a way that the two distances are equal (the embedding f, in this case, is said to be “isometric” or “distance preserving”).
The works on the expressive power of graph neural networks showed that it is possible to construct in polynomial time graph embeddings that satisfy (♠) on a family of graphs on which the Weisfeiler-Lehman test succeeds. This setting seems to be too restrictive. First, it is probably impossible to devise a local and efficient algorithm that guarantees (♠) for all graphs [8]. Second, the graph isomorphism problem does not provide any guarantees for approximately isomorphic graphs, in which case d(G,G′)>0. It is in principle possible, for example, that more similar graphs are less similar in the embedding space, i.e., d(G,G′)<d(G,G″) but |f(G)−f(G′)|>|f(G)−f(G″)|.
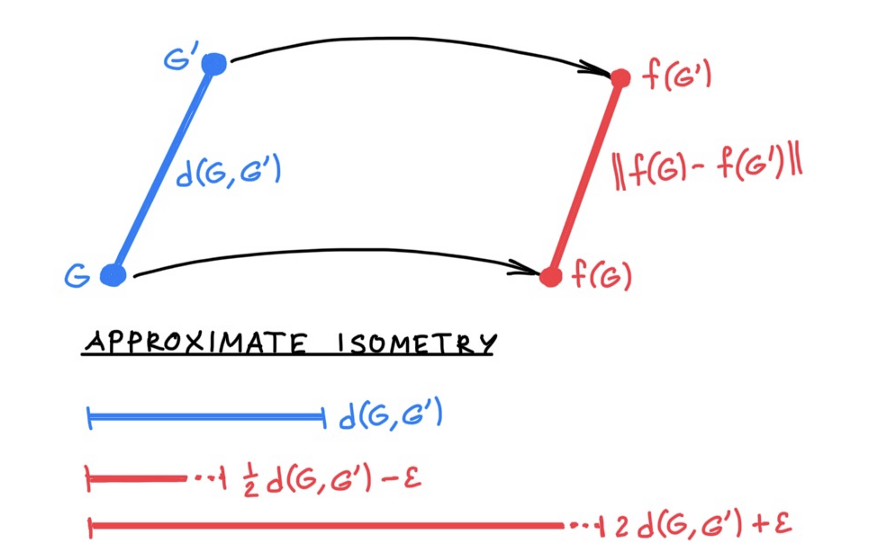
The metric formulation, on the other hand, offers much more flexibility. Instead of requiring (♠) to hold exactly, one can relax it by bounding the metric dilation,
c⁻¹ d(G,G′) ≤ |f(G)−f(G′)| ≤ c d(G,G′) for c≥1 (♣)
which can be expressed as the bi-Lipschitz constant c of the embedding f. This means that the embedding does not “stretch” of “shrink” the groundtruth graph distance d by more than a factor c, which should ideally be as close to 1 as possible. Such an embedding is called an approximate isometry. A result one would try to obtain is a bound c independent of the graphs, and in particular, on the number of vertices.
Note that the graph isomorphism is a particular case of (♣), since for isomorphic graphs G~G′ one has d(G,G′) and thus f(G)=f(G′). As discussed above, this is impossible to achieve for all graphs. Instead, model (♣) can be further relaxed allowing for additional metric distortion ε,
c⁻¹ d(G,G′)−ε ≤ |f(G)−f(G′)| ≤ c d(G,G′)+ε for c≥1 (♦)
which sets a tolerance on how far apart can isomorphic graphs be. This is a small price to pay in many applications if in turn one can possibly satisfy (♦) for a much larger family of graphs than (♠).
Probably approximate isometry. The approximate isomorphism problem can be rewritten as a probabilistic statement in the “probably approximately correct” (PAC) form
( c⁻¹ d(G,G′)−ε ≤ |f(G)−f(G′)| ≤ c d(G,G′) )>1−δ
where the “approximately” is understood in the sense of the metric dilation c and “probably” is that the bound (♦) holds with high probability 1−δ for some distribution of graphs [9]. It is possible that such a setting will turn easier for analysis than the deterministic approximate isometric embedding problem.
Bridging continuous and discrete structures. Last but not least, the question of graph neural network expressivity has been primarily focused on the topology of the graphs. However, in most practical applications, the graphs also have node- or edge-wise features or attributes, typically represented as vectors [10]. The metric framework naturally handles both structures by defining an appropriate distance between attributed graphs.
As a final remark, I remind that one should also bear in mind that the majority of the works on the expressive power of graph neural networks are very recent developments building upon classical results in graph theory. Expanding into additional fields of mathematics such as metric geometry seems a promising avenue that is likely to bear fruit in the near future.
[1] B. Weisfeiler, A. Lehman, The reduction of a graph to canonical form and the algebra which appears therein, 1968 (English translation)
[2] K. Xu et al. How powerful are graph neural networks? (2019). Proc. ICLR.
[3] H. Maron et al. Provably powerful graph neural networks (2019). Proc. NeurIPS.
[4] G. Bouritsas et al. Improving graph neural network expressivity via subgraph isomorphism counting (2020). arXiv:2006.09252.
[5] A. Sanfeliu, K.-S. Fu, A distance measure between attributed relational graphs for pattern recognition (1983). IEEE Trans. Systems, Man, and Cybernetics (3):353–362.
[6] M. Gromov, Structures métriques pour les variétés riemanniennes (1981).
[7] Technically speaking, d is a pseudo-metric and can be regarded as a metric on the quotient set ⧵~ of graphs modulo the isomorphism relation.
[8] I say “probably” because it is still unknown whether the graph isomorphism problem has a polynomial-time solution. It seems extremely unlikely that such a hypothetical algorithm would have practical time and space complexity.
[9] A version of a probabilistic metric setting was previously used to analyse graph kernels in N. M. Kriege et al. A property testing framework for the theoretical expressivity of graph kernels (2018). Proc. IJCAI.
[10] While the Weisfeiler-Lehman framework technically applies to coloured graphs, it is limited to nodes with a discrete set of features.




