Statistical Learning for Data Science

This post covers these topics related to Statistical Learning and their significance in data science.

• Introduction
• Prediction & Inference
• Parametric & Non-parametric methods
• Prediction Accuracy and Model Interpretability
• Bias-Variance Trade-Off

Introduction

Statistical learning is a framework for understanding data based on statistics, which can be classified as supervised or unsupervised. Supervised statistical learning involves building a statistical model for predicting, or estimating, an output based on one or more inputs, while in unsupervised statistical learning, there are inputs but no supervising output; but we can learn relationships and structure from such data.

One of the simple way to understand statistical learning is to determine association between predictors (independent variables, features) & response(dependent variable) and developing a accurate model that can predict response variable (Y) on basis of predictor variables (X).

Y = f(X) + ɛ where X = (X1,X2, . . .,Xp), f is an unknown function & ɛ is random error (reducible & irreducible).

Prediction & Inference

In situations where a set of inputs X are readily available, but the output Y is not known, we often treat f as black box (not concerned with the exact form of f), as long as it yields accurate predictions for Y . This is prediction.

There are situations where we are interested in understanding the way that Y is affected as X change. In this situation we wish to estimate f, but our goal is not necessarily to make predictions for Y . Here we are more interested in understanding relationship between X and Y. Now f cannot be treated as a black box, because we need to know its exact form. This is inference.

In real life, will see a number of problems that fall into the prediction setting, the inference setting, or a combination of the two.

Courtesy: https://www.youtube.com/watch?v=w09Ifi62p8k

Parametric & Non-parametric methods

When we make an assumption about the functional form of f and try to estimate f by estimating the set of parameters, these methods are called parametric methods.

f(X) = β0 + β1X1 + β2X2 + . . . + βpXp

Non-parametric methods do not make explicit assumptions about the form of f, instead they seek an estimate of f that gets as close to the data points as possible.

Courtesy: https://www.slideshare.net/zukun/icml2004-tutorial-on-bayesian-methods-for-machine-learning

Prediction Accuracy and Model Interpretability

Of the many methods that we use for statistical learning, some are less flexible, or more restrictive. When inference is the goal, there are clear advantages to using simple and relatively inflexible statistical learning methods. When we are only interested in prediction, we use flexible models available.

Courtesy: https://towardsdatascience.com/a-complete-machine-learning-walk-through-in-python-part-three-388834e8804b

Assessing Model Accuracy

There is no free lunch in statistics, which means no one method dominates all others over all possible data sets. In the regression setting, the most commonly-used measure is the mean squared error (MSE). In the classification setting, the most commonly-used measure is the confusion matrix. Fundamental property of statistical learning is that, as model flexibility increases, training error will decrease, but the test error may not.

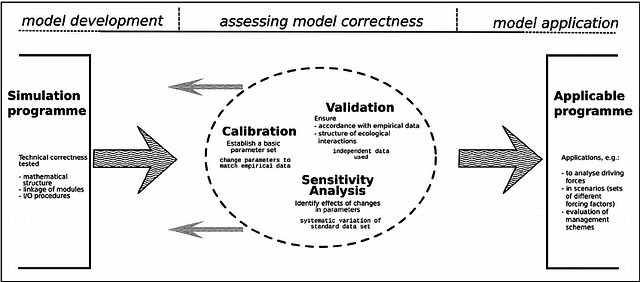
Courtesy: https://www.researchgate.net/figure/Basic-steps-to-assess-model-accuracy-Assuming-a-technically-approved-model-the-next-step_fig1_276365016

Bias & Variance

Bias are the simplifying assumptions made by a model to make the target function easier to learn. Parametric models have a high bias making them fast to learn and easier to understand but generally less flexible. Decision Trees, k-Nearest Neighbors and Support Vector Machines are low-bias machine learning algorithms. Linear Regression, Linear Discriminant Analysis and Logistic Regression are high-bias machine learning algorithms.

Variance is the amount that the estimate of the target function will change if different training data was used. Non-parametric models that have a lot of flexibility have a high variance. Linear Regression, Linear Discriminant Analysis and Logistic Regression are low-variance machine learning algorithms. Decision Trees, k-Nearest Neighbors and Support Vector Machines are high-variance machine learning algorithms.

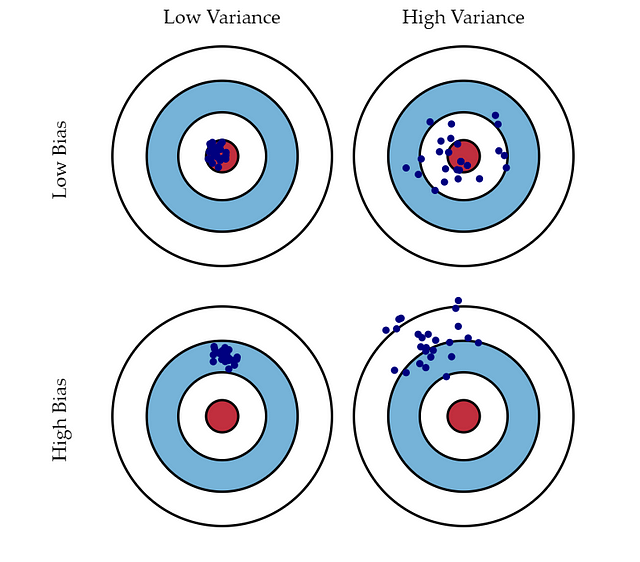
Courtesy: http://scott.fortmann-roe.com/docs/BiasVariance.html

Bias-Variance Trade-Off

The relationship between bias and variance in statistical learning is such that:

• Increasing bias will decrease variance.
• Increasing variance will decrease bias.

There is a trade-off at play between these two concerns and the models we choose and the way we choose to configure them are finding different balances in this trade-off for our problem.

In both the regression and classification settings, choosing the correct level of flexibility is critical to the success of any statistical learning method. The bias-variance trade-off, and the resulting U-shape in the test error, can make this a difficult task.

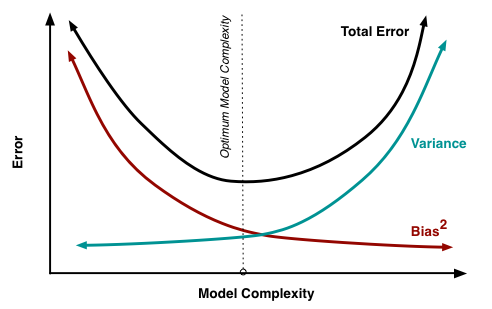
Courtesy: http://scott.fortmann-roe.com/docs/BiasVariance.html