Coding Deep Learning for Beginners — Linear Regression (Part 2): Cost Function

Recap

The last article has introduced the problem which will be solved after Linear Regression implementation is finished. The goal is to predict the prices of Cracow apartments. The dataset consists of samples described by three features: distance_to_city_center, room, and size. To simplify visualizations and make learning more efficient — only size feature will be used.

Additionally, the mathematical formula behind Linear Regression model was presented and explained. For the equation to be complete, it’s parameters needs to have assigned values. Then, the formula is ready to return a numerical prediction for any given input sample.

The two steps described here are called Initialization and Prediction. Both were turned into separate Python functions and used to create a Linear Regression model with all parameters initialized to zeros and used to predict prices for apartments based on size parameter.

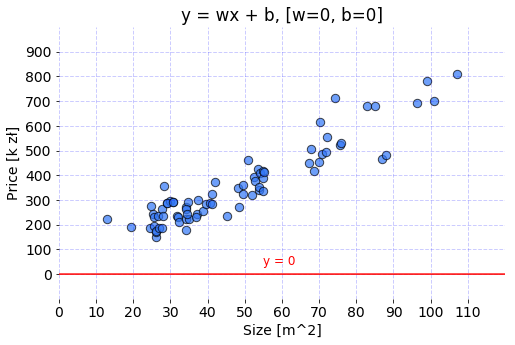
Code used to prepare the graph is available under this link.

Next problem to solve

Model with current parameters will return a zero for every value of area parameter because of all weights of the model and bias equal to zeros. Now let’s modify the parameters and see how the projection of the model changes.

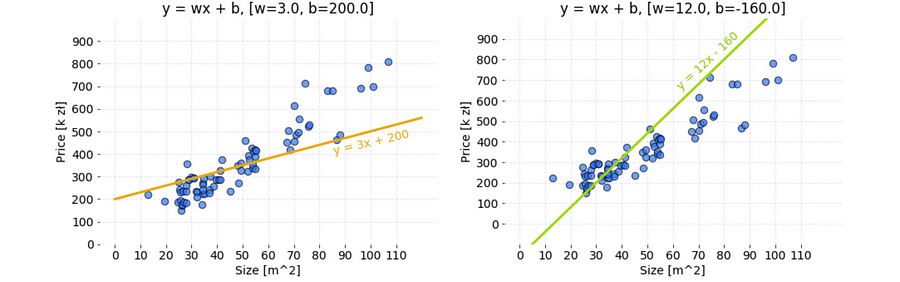
Code used to prepare these graphs is available under this link.

There are two sets of parameters that cause a Linear Regression model to return different apartment price for each value of size feature. Because data has the linear pattern, the model could become accurate approximator of the price after proper calibration of the parameters.

Question to answer

For which set of parameters, the model returns better results?

• Orange: w = 3 , b = 200
• Lime: w = 12 , b = -160

Even though it might be possible to guess the answer by visual judgment correctly, the computer doesn’t imagine — it compares the values. This is where cost Cost Function comes to help.

Cost Function

It is a function that measures the performance of a Machine Learning model for given data. Cost Function quantifies the error between predicted values and expected values and presents it in the form of a single real number. Depending on the problem Cost Function can be formed in many different ways. The purpose of Cost Function is to be either:

• Minimized – then returned value is usually called cost, loss or error. The goal is to find the values of model parameters for which Cost Function return as small number as possible.
• Maximized – then the value it yields is named a reward. The goal is to find values of model parameters for which returned number is as large as possible.

For algorithms relying on Gradient Descent to optimize model parameters, every function has to be differentiable.

Tailoring Cost Function

Given a model using the following formula:

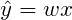
where:

• ŷ – predicted value,
• x – vector of data used for prediction or training,
• w – weight.

Notice that bias parameter is omitted on purpose. Let’s try to find the value of weight parameter, so for the following data samples:

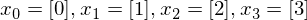
the outputs of the model are as close as possible to:

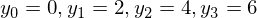
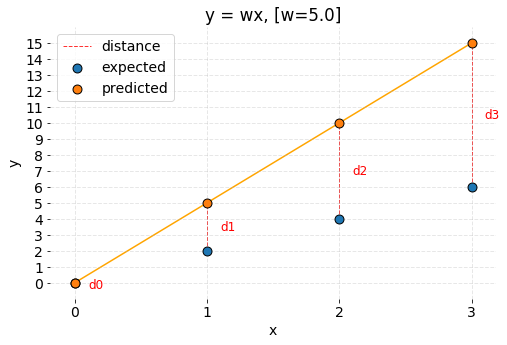
Now it’s time to assign a random value to weight parameter and visualize the results of the model. Let’s pick w = 5.0 for now.

Code used to prepare the graph is available under this link.

It can be observed that model predictions are different than expected values. How can it be expressed mathematically? The most straightforward idea is to subtract both values from each other and see if the result of that operation equals zero. Any other result means that the values differ. The size of the received number provides information about how significant the error is. From the geometrical perspective, it is possible to state that error is the distance between two points in the coordinate system. Let’s define the distance as:

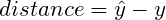
According to the formula, calculate the errors between the predictions and expected values:

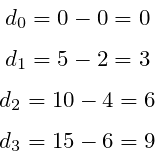
As it was stated before, Cost Function is a single number describing model performance. Therefore let’s sum up the errors.

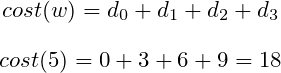
However, now imagine there are a million points instead of four. The accumulated errors would become a bigger number for model making a prediction on larger dataset than on a smaller dataset. Consequently, those models could not be compared. That’s why it has to be scaled in some way. The right idea is to divide the accumulated errors by the number of points. Cost stated like that is mean of errors that model has made for given dataset.

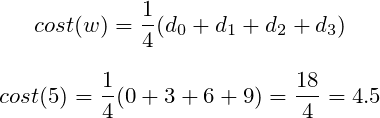
Unfortunately, the formula is unfinished yet. Before that, all cases have to be considered so let’s try picking smaller weight now and see if the created Cost Function works. Now, weight is about to be set to w = 0.5 .

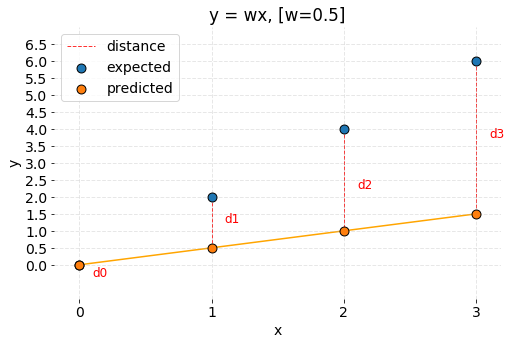
Code used to prepare the graph is available under this link.

The predictions are off again. However, what’s different in comparison to the previous case is that predicted points are below expected points. Numerically predictions are smaller. The cost formula is going to malfunction because calculated distances have negative values.

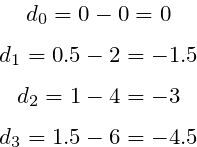
The cost value is also negative:

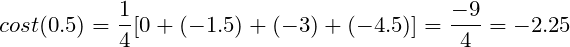
It is incorrect to say that distance can have negative value. It is possible to attach a more substantial penalty to the predictions that are located above or below the expected results (some cost functions do so, e.g. RMSE), but the value shouldn’t be negative as it will cancel out positive errors. Then it is going to become impossible to properly minimize or maximize the Cost Function.

So how about fixing the problem by using the absolute value of the distance? After stating the distance as:

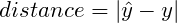
The costs for each value of weights are:

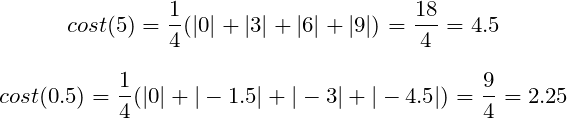
Now the costs for both weights w = 5.0 and w = 0.5 are correctly calculated. It is possible to compare the parameters. The model achieves better results for w = 0.5 as the cost value is smaller.

The function that was created is called Mean Absolute Error.

Mean Absolute Error

Regression metric which measures the average magnitude of errors in a group of predictions, without considering their directions. In other words, it’s a mean of absolute differences among predictions and expected results where all individual deviations have even importance.

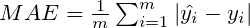
where:

• i – index of sample,
• ŷ – predicted value,
• y – expected value,
• m – number of samples in dataset.

Sometimes it is possible to see the form of formula with swapped predicted value and expected value, but it works the same.

Let’s turn math into the code:

The function takes as an input two arrays of the same size: predictions and targets. The parameter m of the formula, which is the number of samples, equals to the length of sent arrays. Thanks to the fact that arrays have the same length it is possible to iterate over both of them at the same time. The absolute value of the difference between each prediction and target is calculated and added to accumulated_error variable. After gathering errors from all pairs, the accumulated result is averaged by the parameter m which returns MAE error for given data.

Mean Squared Error

One of the most commonly used and firstly explained regression metrics. Average squared difference between the predictions and expected results. In other words, an alteration of MAE where instead of taking the absolute value of differences, they are squared.

In MAE, the partial error values were equal to the distances between points in the coordinate system. Regarding MSE, each partial error is equivalent to the area of the square created out of the geometrical distance between the measured points. All region areas are summed up and averaged.

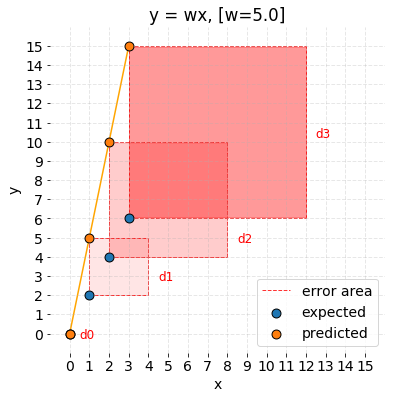
Code used to prepare the graph is available under this link.

The MSE formula can be written like this:

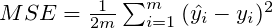
• i – index of sample,
• ŷ – predicted value,
• y – expected value,
• m – number of samples in dataset.

There are different forms of MSE formula, where there is no division by two in the denominator. Its presence makes MSE derivation calculus cleaner.

Calculating derivative of equations using absolute value is problematic. MSE uses exponentiation instead and consequently has good mathematical properties which make the computation of it’s derivative easier in comparison to MAE. It is relevant when using a model that relies on the Gradient Descent algorithm.

MSE can be written in Python as follows:

The only distinctions from, introduced in the previous paragraph, mae(predictions, targets) function are:

• difference between prediction and target is squared,
• 2 in the averaging denominator.

Differences between MAE and MSE

There is much more regression metrics that can be used as Cost Function for measuring the performance of models that try to solve regression problems (estimating the value). MAE and MSE seem to be relatively simple and very popular.

Why there are so many metrics?

Each metric treats the differences between observations and expected results in a unique way. The distance between ideal result and predictions are having attached a penalty by metric, based on the magnitude and direction in the coordinate system. For example, a different metric such as RMSE more aggressively penalizes predictions which values are lower than expected than those which are higher. Its usage might lead to the creation of a model which returns inflated estimations.

How MAE and MSE are treating the differences between the points? To check it, let’s calculate the cost for different weight values:

Table presents the errors of many models created with different weight parameter. Cost of each model was calculated with both MAE and MSE metrics.

And display it on the graphs:

The graphs show how metric value change for different values of parameter w. Code used to prepare these graphs is available under this link.

It is possible to observe that:

• MAE doesn’t add any additional weight to the distance between points — the error growth is linear.
• MSE errors grow exponentially with larger values of distance. It’s a metric that adds a massive penalty to points which are far away and a minimal penalty for points which are close to the expected result. Error curve has a parabolic shape.

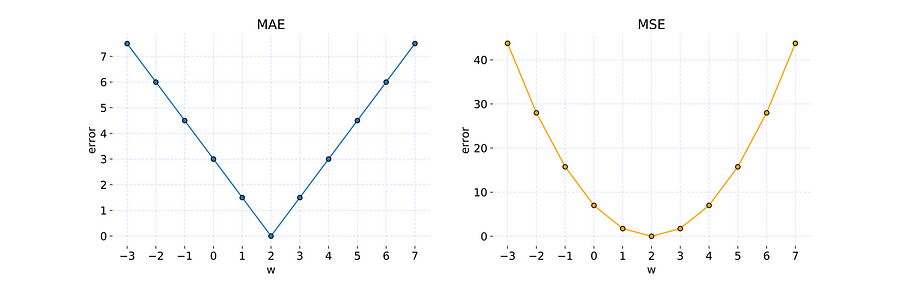
Additionally, by checking various weight values, it was possible to find the parameter for error is equal to zero. If the w = 2.0 is used to build the model, then the predictions look as following:

Code used to prepare the graph is available under this link.

When predictions and expected results overlap, then the value of each reasonable Cost Function is equal to zero.

Answer

It’s high time to answer the question about which set of parameters, orange or lime, creates better approximator for prices of Cracow apartments. Let’s use MSE to calculate the error of both models and see which one is lower.

Majority of the code was explained in the previous article. Instead of calling init(n) function, parameter dictionaries were created manually for testing purposes. Notice that both models use bias this time. Function predict(x, parameters) was used for the same data with different parameters argument. Then resulting predictions named orange_pred and lime_pred became an argument for mse(predictions, targets) function which returned error value for each model separately.

The results are as following:

• orange: 4909.18
• lime: 10409.77

which means that orange parameters create better model as the cost is smaller.

Summary

In this article, I have explained the idea of Cost Function — a tool which allows us to evaluate model parameters. I have introduced you to two most often used regression metrics MAE and MSE.

In the next article, I am going to show you how to train model parameters with Gradient Descent algorithm.