This is the first in the series of three posts on the expressivity of graph neural networks
Do you have a feeling that deep learning on graphs is a bunch of heuristics that work sometimes and nobody has a clue why? In this post, I discuss the graph isomorphism problem, the Weisfeiler-Lehman heuristic for graph isomorphism testing, and how it can be used to analyse the expressive power of graph neural networks.
Traditional feed-forward networks (multi-layer perceptrons) are known to be universal approximators: they can approximate any smooth function to any desired accuracy. For graph neural networks, which have emerged relatively recently, the representation properties are less understood. It often happens to observe in experiments that graph neural networks excel on some datasets but at the same time perform disappointingly on others. In order to get to the root of this behaviour, one has to answer the question: how powerful are graph neural networks?
One of the challenges is that graphs encountered in applications are combinations of continuous and discrete structures (node- and edge features and connectivity, respectively), and thus this question can be posed in different ways. One possible formulation is whether graph neural networks can distinguish between different types of graph structures. This is a classical question in graph theory known as the graph isomorphism ; problem, aiming to determine whether two graphs are topologically equivalent [1]. Two isomorphic graphs have the same connectivity and differ only by a permutation of their nodes.
Somewhat surprisingly, the exact complexity class of the graph isomorphism problem is unknown. It is not known to be solvable in polynomial time nor to be NP-complete and is sometimes attributed to a special “GI class” [2].
Weisfeiler-Lehman test
The seminal 1968 paper of Boris Weisfeiler and Andrey Lehman [3] proposed an efficient heuristic now known as the Weisfeiler-Lehman (WL) test that was initially believed to be a polynomial-time solution for the graph isomorphism problem [4]. A counter example was found a year later; however, it appears that the WL test works for almost all graphs, in the probabilistic sense [5].
Expressive Power Of Graph Neural Networks And The Weisfeiler-Lehman Test
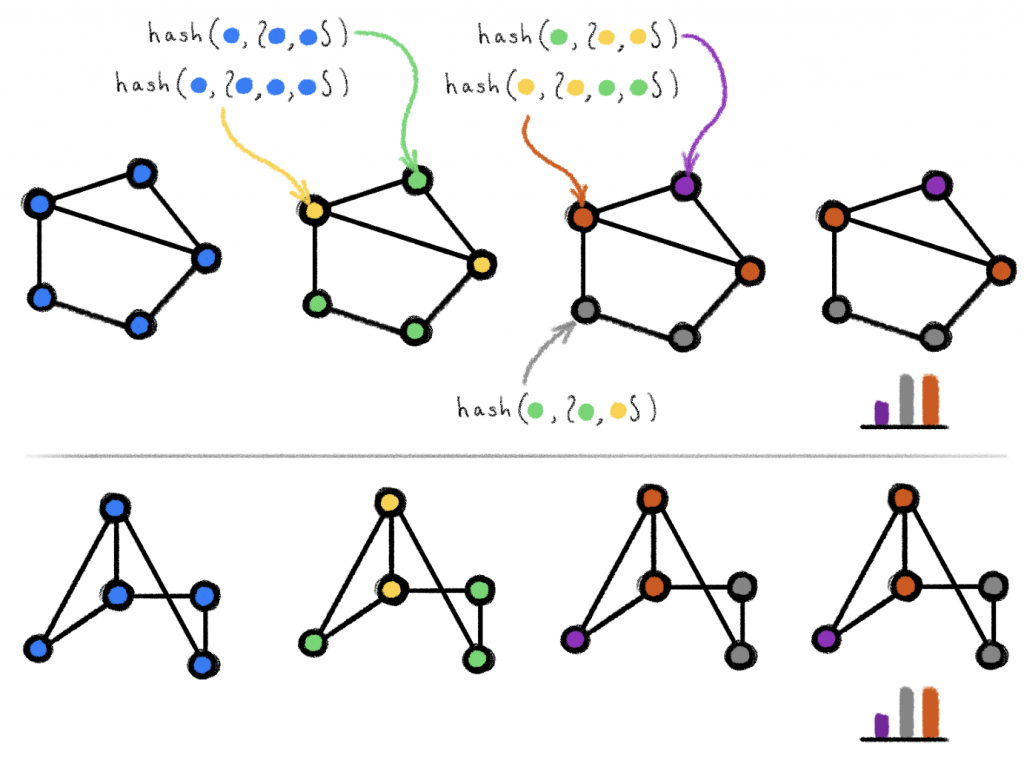
Example of execution of the Weisfeiler-Lehman test on two isomorphic graphs. Curled brackets denote multisets. The algorithm stops after the colouring does not change and produces an output (histogram of colours). Equal outputs for the two graphs suggest that they are possibly isomorphic.
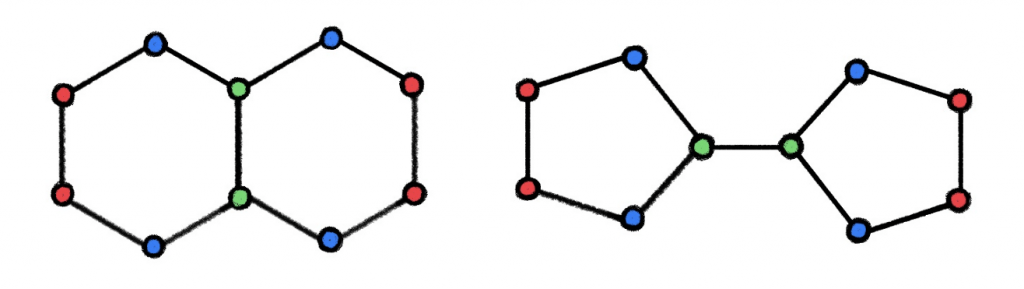
The WL test is based on iterative graph recolouring [6] (“colour” in graph theory refers to a discrete node label), starting with all nodes of identical colour. At each step, the algorithm aggregates the colours of nodes and their neighbourhoods representing them as multisets [7], and hashes the aggregated colour multisets into unique new colours. The algorithm stops upon reaching a stable colouring. If at that point the colourings of the two graphs differ, the graphs are deemed non-isomorphic. However, if the colourings are the same, the graphs are possibly (but not necessarily) isomorphic. In other words, the WL test is a necessary but insufficient condition for graph isomorphism. There exist non-isomorphic graphs for which the WL test produces identical colouring and thus considers them “possibly isomorphic”; the test is said to fail in this case. One such example is shown in the following figure:
Expressive Power Of Graph Neural Networks And The Weisfeiler-Lehman Test
Two non-isomorphic graphs on which the WL graph isomorphism test fails, as evident from the identical colouring it produces. In chemistry, these graphs represent the molecular structure of two different compounds, decalin (left) and bicyclopentyl (right). Figure adapted from [14].
Graph isomorphism networks
Keyulu Xu [9] and Christopher Morris [10] (and at least two years earlier, Thomas Kipf in his blog post) noticed that the WL test bears striking resemblance to graph message passing neural networks [8], a way of doing convolution-like operations on graphs. In a message-passing layer, the features of each node are updated by aggregating the features of the neighbours. The choice of the aggregation and the update operations is crucial: only multiset injective functions make it equivalent to the WL algorithm. Some popular choices for aggregators used in the literature such as maximum or mean are actually strictly less powerful than WL and fail to distinguish between very simple graph structures:
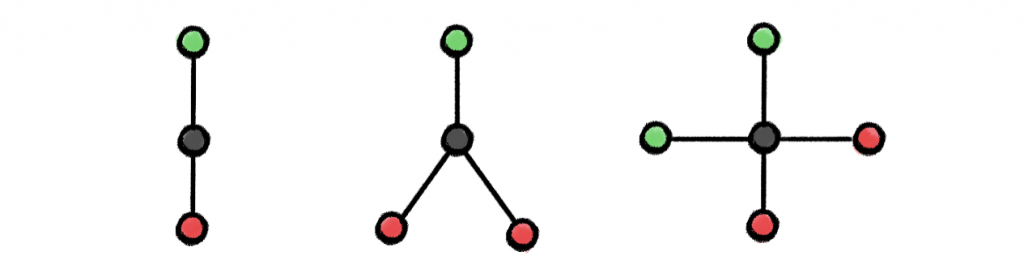
Expressive Power Of Graph Neural Networks And The Weisfeiler-Lehman Test
Examples of graph structures that cannot be distinguished by max but can be distinguished by the mean aggregator (first and second) and can be distinguished by neither max nor mean (first and third). The reason is that the features aggregated in this way from the neighbours of the black node will be the same. Figure adapted from [9].
Xu proposed a choice of the aggregation and update functions that make message passing neural networks equivalent to the WL algorithm, calling them Graph Isomorphism Networks (GIN). This is as powerful as a standard message-passing neural network can get. But more than a new architecture, the main impact was formulating the question of expressiveness in a simple setting that could be related to a classical problem from graph theory. This idea has already spurred multiple follow-up works.
Weisfeiler-Lehman hierarchy
One direction of extending the results of Xu and Morris was using more powerful graph isomorphism tests. Proposed by László Babai, the k-WL test is a higher-order extension of the Weisfeiler-Lehman algorithm that works on k-tuples instead of individual nodes. With the exception of 1-WL and 2-WL tests that are equivalent, (k+1)-WL is strictly stronger than k-WL, for any k≥2, i.e. there exist examples of graphs on which k-WL fails and (k+1)-WL succeeds, but not vice versa. k-WL is thus a hierarchy or increasingly more powerful graph isomorphism tests, sometimes referred to as the Weisfeiler-Lehman hierarchy [10].
It is possible to design graph neural networks that follow the k-WL test and are thus strictly more powerful than message passing architectures. One such first architecture,k-GNN, was proposed by Morris [11]. A key difference between traditional message passing neural networks and such higher-order GNNs is the fact that they are non-local, as thek-WL algorithm operates on k-tuples of nodes. This has significant implications both on the implementation of the algorithm and its computational and memory complexity: k-GNNs require (nᵏ) memory. As a way of mitigating complexity, Morris devised a local version of k-GNNs based on aggregation in local neighbourhoods, which however is less expressive thank-WL.
Somewhat different high-order graph architectures were proposed by Haggai Maron, in whose Ph.D. defence at Weizmann Institute I had the privilege to participate in September 2019. Maron defined a class of Invariant Graph Networks (IGN) based on k-order tensors [12] and showed they are as powerful as k-WL. IGNs are derived from a different variant of k-WL [10] and are more advantageous in terms of their complexity compared to k-GNNs. In particular, the 3-WL-equivalent IGN has “only” quadratic complexity, which is probably the only practically useful graph neural network architecture strictly more powerful than message passing, but still a far cry from the linear complexity of the former[16].
From a theoretical standpoint, the works on provably powerful graph neural networks provided a rigorous mathematical framework that can help interpret and compare different algorithms. There have been multiple follow-up works that extended these results using methods from graph theory and distributed local algorithms [14].
From a practical standpoint, however, there has hardly been a significant impact of these new architectures: for example, the latest benchmarks [15] show that recent provably powerful algorithms actually underperform older techniques. This is not an uncommon situation in machine learning where there are often big gaps between theory and practice. One of the explanations could be deficiencies in the benchmark itself. But perhaps more profound reasons are that better expressivity does not necessarily offer better generalisation (sometimes quite the opposite), and moreover, it is possible that the graph isomorphism model might not capture correctly the actual notion of graph similarity in specific applications — I will discuss this in my next posts. For sure, this line of works is extremely fruitful for building bridges to other disciplines and bringing methods previously not used in the field of deep learning on graphs [17]
I.e. there exists an edge-preserving bijection between the nodes of the two graphs.
The graph isomorphism is thus possibly an ;NP-intermediatecomplexity class. For some special families of graphs (e.g. trees, planar graphs, or graphs of bounded maximum degree), there exist polynomial-time algorithms.
B. Weisfeiler, A. Lehman, The reduction of a graph to canonical form and the algebra which appears therein (1968). Nauchno-Technicheskaya Informatsia 2(9):12–16. ;English translation and the original Russian version, which contains a pun in the form of an unusual Cyrillic notation (Операция „Ы“) referring to the eponymous Soviet blockbuster from three years earlier. See also a popular exposition in this blog post. Lehman is sometimes also spelled “Leman”, however, given the Germanic origin of the surname, I prefer the more accurate former variant.
I. Ponomarenko, The original paper by Weisfeiler Lehman. Provides the historical context of this classical paper. He points out that the motivation for the work came from chemical applications.
L. Babai et al. Random graph isomorphism(1980). SIAM J. Computing 9(3):628–635.
The original paper of Weisfeiler and Lehman actually described the 2-WL variant, which is however equivalent to 1-WL, also known as the colour refinement algorithm. As a historical note, such algorithms have been known in computational chemistry before, see e.g. H. L. Morgan. The generation of a unique machine description for chemical structures — a technique developed at chemical abstracts service (1965). J. Chem. Doc. 5(2):107–113, which lies at the foundation of the Morgan molecular fingerprints broadly used in chemistry.
A multiset is a set where the same element may appear multiple times but the order of the elements does not matter.
J. Gilmer et al., Neural message passing for quantum chemistry
K. Xu et al. (2019). Proc. ICLR.
There exist several variants of WL tests that have different computational and theoretical properties, and the terminology is rather confusing: readers are advised to clearly understand what exactly different authors mean by “k-WL”. Some authors, e.g. Sato and Maron, distinguish between WL and “folklore” WL (FWL) tests, which mainly differ in the colour refinement step. The k-FWL test is equivalent to (k=+1)-WL. The set k-WL algorithm used by Morris is another variant that has lower memory complexity but is strictly weaker than k-WL.
C. Morris et al. ;Weisfeiler and Leman go neural: Higher-order graph neural networks
H. Maron et al. (2019). Proc. ICLR.
H. Maron et al. Provably powerful graph neural networks (2019). Proc. NeurIPS. See also a blog post of the authors
R. Sato, A survey on the expressive power of graph neural networks (2020). Provides a very comprehensive review of different WL tests and equivalent graph neural network architectures, as well as links to distributed computing algorithms.
V. P. Dwivedi et al. Benchmarking graph neural networks (2020).
More precisely, the complexity of message passing is linear in the number of edges, not nodes. In sparse graphs, this is roughly the same. In dense graphs, the number of edges can be of (n²). For this reason, Maron suggests his architecture could be useful for dense graphs.
To be historically accurate, the WL formalism is not new to the machine learning community. The seminal paper of N. Shervashidze and K. M. Borgwardt, Fast subtree kernels on graphs (2009). Proc. NIPS was, to the best of my knowledge, the first to use this construction before the recent resurgence of deep neural networks and precedes the works discussed in this post by nearly a decade.
I am grateful to Mehdi Bahri, Luca Belli, Giorgos Bouritsas, Fabrizio Frasca, Ferenc Huszar, Sergey Ivanov, Emanuele Rossi, and David Silver for their help with proof-reading and editing this post, and to Karsten Borgwardt for pointing the relation to WL kernels. A Chinese translation of this post is available by courtesy of Zhiyong Liu.