A simple study on how to check the statistical goodness of a regression model.
Photo by Antoine Dautry on Unsplash
Regression models are very useful and widely used in machine learning. However, they might show some problems when comes to measure the goodness of a trained model. While classification models have some standard tools that can be used to assess their performance (i.e. area under the ROC curve, confusion matrix, F-1 score etc.), regression models’ performance can be measured in many different ways. In this article, I’ll show you some techniques I’ve used in my experience as a Data Scientist.
Example in R
In this example, I’ll show you how to measure the goodness of a trained model using the famous iris dataset. I’ll use a linear regression model to predict the value of the Sepal Length as a function of the other variables.
First, we’ll load the iris dataset and split it in training and holdout.
set.seed(1)training_idx = sample(1:nrow(iris),nrow(iris)*0.8,replace=FALSE)
holdout_idx = setdiff(1:nrow(iris),training_idx)training = iris[training_idx,]
holdout = iris[holdout_idx,]
Then we can perform a simple linear regression in order to describe the variable Sepal.Length as a linear function of the others. This is the model we want to check the goodness of.
m = lm(Sepal.Length ~ .,training)
All we need to do now is compare the residuals in the training set with the residuals in the holdout. Remember that the residuals are the differences between the real value and the predicted value.
holdout_res = holdout$Sepal.Length – predict(m,holdout)
If our training procedure has produced overfitting, the residuals in the training set will be very small compared with the residuals in the holdout. That’s a negative signal that should invite us to simplify the model or remove some variables.
Let’s now perform some statistical checks.
t-test
The first thing we have to check is whether the residuals are biased or not. We know from elementary statistics that the mean value of the residuals is zero, so we can start checking with a Student’s t-test if it’s true or not for our holdout sample.
t.test(holdout_res,mu=0)

As we can see, the p-value is greater than 5%, so we cannot reject the null hypothesis and can say that the mean value of the holdout residuals is statistically similar to 0.
Then, we can test if the holdout residuals have the same average as the training ones. This is called Welch’s t-test.
t.test(training_res,holdout_res)

Again, a p-value higher than 5% can make us tell that there aren’t enough reasons to assume that the mean values are different.
F-test
`
After we have checked the mean value, there comes the variance. We obviously want that the holdout residuals show a behavior not so much different from the training residuals, so we can compare the variances of the two sets and check whether the holdout variance is higher than the training variance.
A good test to check if a variance is greater than another one is the F-test, but it only works with normally distributed residuals. If the distribution is not normal, the test might give wrong results.
So, if we really want to use this test, we must check the normality of the residuals using (for example) a Shapiro-Wilk test.
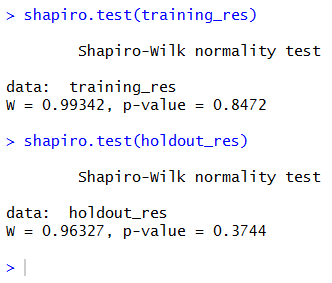
Both p-values are higher than 5%, so we can say that both sets show normally distributed residuals. We can safely go on performing the F-test.
var.test(training_res,holdout_res)

The p-value is 72%, which is greater than 5% and allows us to say that the two sets have the same variance.
Kolmogorov-Smirnov test
KS test is very general and useful for many situations. Generally speaking, we expect that, if our model works well, the probability distribution of the holdout residuals is similar to the probability distribution of the training residuals. The KS test has been created to compare probability distributions, so it can be used for this purpose. However, it carries some approximations that can be dangerous to our analysis. Significative differences between probability distributions can be hidden in the general considerations made by the test. Last, KS distribution is known only with some kind of approximation and, consequently, the p-value; so I suggest to use this test with care.
ks.test(training_res,holdout_res)

Again, the large p-value can make us tell that the two distributions are the same.
Plot
A Professor of mine at the University usually said: “you have to look at data by your eyes”. In machine learning, it’s definitely true.
The best way to take a look at a regression data is by plotting the predicted values against the real values in the holdout set. In a perfect condition, we expect that the points lie on the 45 degrees line passing through the origin (y = x is the equation). The nearer the points to this line, the better the regression. If our data make a shapeless blob in the Cartesian plane, there is definitely something wrong.
abline(0,1)
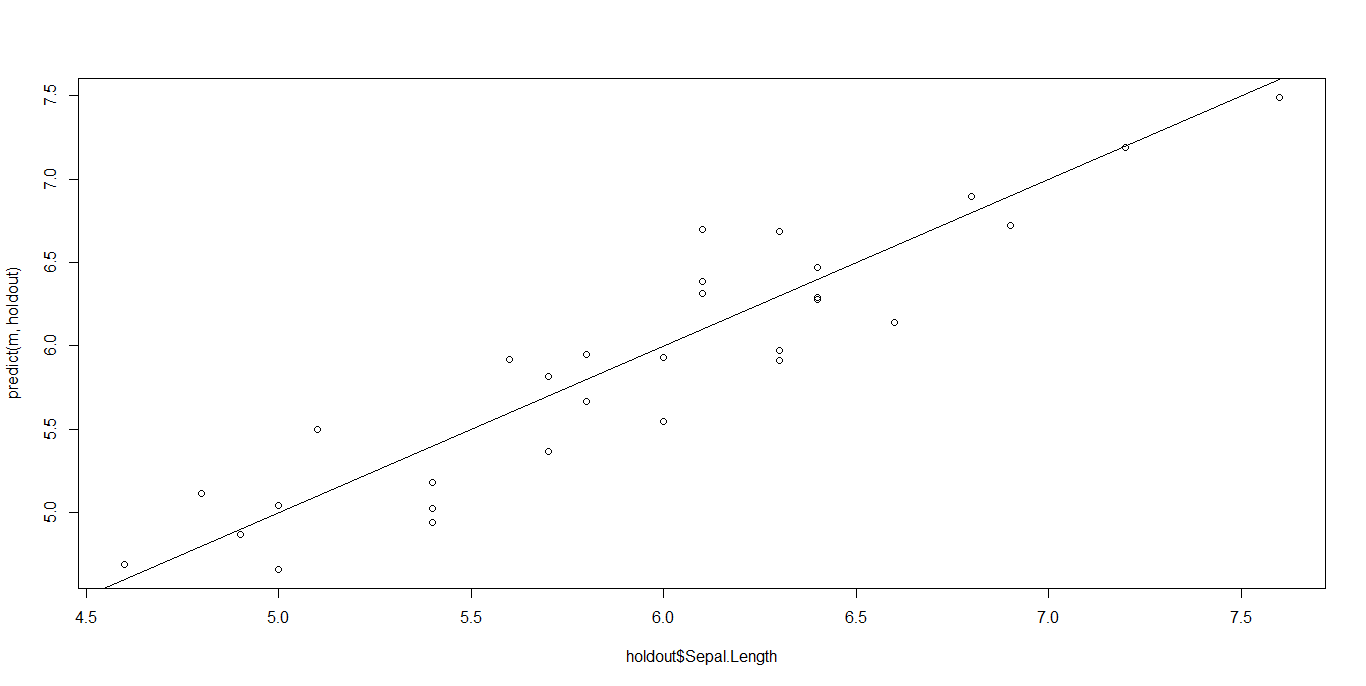
Well, it could have been better, but it’s not completely wrong. Points lie approximatively on the straight line.
t-test on plot
Finally, we can calculate a linear regression line from the previous plot and check if its intercept is statistically different from zero and its slope is statistically different from 1. To perform these checks, we can use a simple linear model and the statistical theory behind the Student’s t-test.
Remember the definition of the t variable with n-1 degrees of freedom:
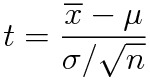
When we use the summarize function of R on a linear model, it gives us the estimates of the parameters and their standard errors (i.e. the complete denominator of the t definition).
For the intercept, we have mu = 0, while the slope has mu = 1.
s = summary(test_model)intercept = s$coefficients[“(Intercept)”,”Estimate”]
intercept_error = s$coefficients[“(Intercept)”,”Std. Error”]
slope = s$coefficients[“predicted”,”Estimate”]
slope_error = s$coefficients[“predicted”,”Std. Error”]t_intercept = intercept/intercept_errort_slope = (slope-1)/slope_error
Now we have the t values, so we can perform a two-sided t-test in order to calculate the p-values.

They are greater than 5% but not too high in absolute value.
Which method is the best one?
As usual, it depends on the problem. If the residuals are normally distributed, t-test and F-test are enough. If they are not, maybe a first plot can help us discover a macroscopic bias before using a Kolmogorov-Smirnov test.
However, non-normally distributed residuals should always raise an alarm in our head and make us search for some hidden phenomenon we haven’t considered yet.
Conclusions
In this short article, I’ve shown you some methods to calculate the goodness of a regression model. Though there are many possible ways to measure it, these simple techniques can be very useful in many situations and easily explainable to a non-technical audience.